因数分解はちょうど展開と反対の計算です。 整式をより次数の低い整式に分解します。 非常に重要な計算なのでしっかり学習していきましょう。
目次
因数分解
整式をより次数の低い整式の積に分解することを因数分解といいます。 例えば\(x^2 + 5x + 4 = (x + 1)(x + 4)\)という計算です。 ちょうど整式の展開とは反対の計算ですね。
この時点では因数分解が何に役立つか実感できないと思いますが, 因数分解は方程式を解くときに非常に役立ちます。 その説明はのちのち2次方程式と一緒に行います。
ここではまず因数分解の方法を覚えておきましょう。
分解して出てきた各パーツを因数といいます。 \(x^2 + 5x + 4 = (x + 1)(x + 4)\)でいえば\(x + 1\)と\(x + 4\)が因数です。
次は下の式を見てください。
左辺の項\(xy, xz\)の両方ともに\(x\)という因数が含まれていますね。 こんなとき,分配法則の反対の計算によって右辺のように因数分解できます。
このように整式のすべての項に含まれている因数を共通因数と呼びます。 共通因数が見つかれば上の例のように因数分解ができます。これを共通因数\(x\)で「くくる」といいます。 最も基本的な因数分解ですね。
また,因数分解は何回かできるかもしれません。 できるところまで因数分解するようにしましょう。
ここでは係数が有理数の範囲で因数分解することにします。 このとき\(x + 1\)や\(x^2 + x + 5\)のように,最終的にはそれ以上因数分解できない整式が出てきます。 有理数についてはまた後で説明しますが,今は気にしなくてOKです。
ここからは因数分解の例をみていきましょう。
平方の形へ因数分解
平方公式の反対の計算です。
- \(a^2 + 2ab + b^2 = (a + b)^2\)
- \(a^2 - 2ab + b^2 = (a - b)^2\)
\(\textcolor{red}{x^2} + 4xy + \textcolor{red}{4y^2}\)のように2乗の項が2つ(\(x^2\)と\((2y)^2\))あるときは,この因数分解が使えないか確認してみましょう。
この場合\(a\)の部分が\(x\),\(b\)の部分が\(2y\)です。 あとは\(2ab\)の部分が\(4xy\)と一致するか確認すれば良いですね。
実際に確かめてみると,\(2 \cdot x \cdot 2y = 4xy\)なので公式の形にバッチリ合います。 これで\(x^2 + 4xy + 4y^2 = (x + 2y)^2\)と因数分解できることが分かりました。
和と差の積へ因数分解
和と差の積の反対の計算です。
\(a^2 - b^2 = (a + b)(a - b)\)
これは非常に簡単で,2乗と2乗の差の形であれば因数分解できます。
2つほど例を挙げておきます。
1次式の積へ因数分解
1次式の積の反対の計算です。 よく使います。
\(\begin{align}&x^2 + (a + b)x + ab \\[5pt]&= (x + a)(x + b)\end{align}\)
\(x^2 + 8x + 15\)を例に考えます。 足して\(8\),掛けて\(15\)になる数を探せば良いわけですね。 足して\(8\)になる数はたくさんありますから掛けて\(15\)になる数から考えます。
掛けて\(15\)になる数は\((1, 15), (3, 5), (-1, -15), (-3, -5)\)の4通りです。 この中から足して\(8\)になるものを探すと\((3, 5)\)だけがあてはまります。 これで\(x^2 + 8x + 15 = (x + 3)(x + 5)\)と因数分解できることが分かりました。
この例のようにまず定数項を作る数の組み合わせを考えて, その候補の中から\(x\)の係数を作る数の組み合わせを見つけましょう。
もう1つの例として\(x^2 - 5xy + 6y^2\)の因数分解を考えましょう。 文字が2つありますが\(x\)だけに着目すると分かりやすいです。
足して\(-5y\),掛けて\(6y^2\)となる数を探しましょう。 まず掛けて\(6y^2\)となる数を考えますが,\((6, y^2)\)のような組み合わせは足しても\(-5y\)になりえません。 \((\triangle y, \Box y)\)の組み合わせだけ考えます。
そうすると考えられる組み合わせは\((y, 6y), (2y, 3y), (-y, -6y), (-2y, -3y)\)だけです。 この中で足して\(-5y\)になるのは\((-2y, -3y)\)です。 これで\(x^2 - 5xy + 6y^2 = (x - 2y)(x - 3y)\)と因数分解できました。
たすき掛け
1次式の積の反対の計算ですが,少し難しいパターンです。
\(\begin{align}&acx^2 + (ad + bc)x + bd \\[5pt]&= (ax + b)(cx + d)\end{align}\)
今度は\(x^2\)の係数が\(1\)ではありません。 掛けて定数項になる数とともに,掛けて\(x^2\)の係数になる数も考えなければならず複雑です。 そこでよく使われるのがたすき掛けという方法です。
たすき掛けは本当は必要ありません。 公式の\(a, b, c, d\)に当てはまる数の組み合わせさえ見つかればOKです。
例として\(4x^2 + 5x - 6\)の因数分解を考えます。 \(x^2\)の係数が\(4\)なので,因数分解すると\((x + \triangle)(4x + \Box)\)か\((2x + \triangle)(2x + \Box)\)という形になります。
あとは\(\triangle\)と\(\Box\)の組み合わせを考えるだけですが,これらの積が定数項\(-6\)なのですから,その組み合わせもかなり絞られてきます。 その中で展開後の\(x\)の係数が\(5\)になるような\(\triangle\)と\(\Box\)を暗算で探せばOKです。
展開後の\(x\)の係数は,\((x + \triangle)(4x + \Box)\)であれば\(4\triangle + \Box\)ですね。 これが\(5\)にならないか幾つか試してみると,\(4x^2 + 5x - 6 = (x + 2)(4x - 3)\)と因数分解できることが分かります。
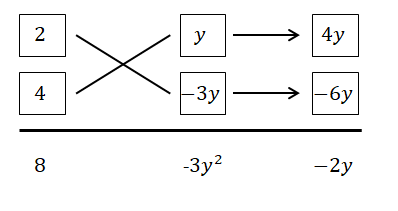
実は,たすき掛けはこの計算を図にしたものです。 なので上記の暗算ができる人には,たすき掛けは必要ありません。 逆に暗算で混乱する人にとっては,たすき掛けが役立ちます。
\(4x^2 + 5x - 6\)を例にたすき掛けを試してみましょう。 次のような図を書いておいてください。(赤文字は書かなくても良いです。) 赤文字は,公式中の\(a, b, c, d\)に対応しています。
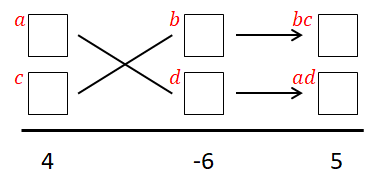
この図の説明をします。
- 下側の数字は左から順に\(x^2\)の係数,定数項,\(x\)の係数です。
- 左2つの四角には掛けて\(4\)(\(x^2\)の係数)になる数\(a, c\)を入れます。
- 真ん中2つの四角には掛けて\(-6\)(定数項)になる数\(b, d\)を入れます。
- 右2つの四角には\(ad\)と\(bc\)を入れ,\(ad + bc\)が\(5\)(\(x\)の係数)になるか確認します。
これからこの図の穴埋めをしていきます。
まず掛けて\(x^2\)の係数になる数を考えます。 この場合は掛けて\(4\)になるので\((1, 4), (2, 2)\)です。 次の補足の通り\((-1, -4), (-2, -2)\)は考えなくてOKです。
掛けて\(x^2\)の係数になる負の数を考えても意味がありません。 例えば\((-x - 2)(-4x + 3)\)は\((x + 2)(4x - 3)\)と変形できます。 このように掛けて\(x^2\)の係数になる数は最初から正の数でとることができるのです。
ただし掛けて定数項になる数については,負の数も含めて考える必要があります。
またそもそも\(x^2\)の係数が負の場合は, 例えば\(-4x^2 - 5x + 6 = -(4x^2 + 5x - 6)\)のように式全体をマイナスでくくってしまえば, 掛けて\(x^2\)の係数になる負の数を考えずに済みます。
候補が\((1, 4), (2, 2)\)の2つ見つかりましたが,まだどちらが正解かは分かりません。 分からないので順番に確かめます。 まずは\((1, 4)\)の方を確かめてみましょう。先ほどの図に\((1, 4)\)を入れます。
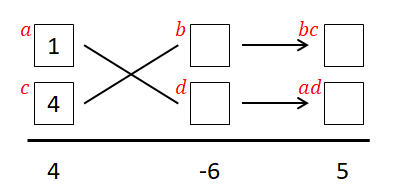
次は掛けて定数項になる数を考えます。 この場合は掛けて\(-6\)になるので\((1, -6), (-1, 6), (2, -3), (-3, 2)\)です。 まだどれが正解かは分かりません。まずは\((1, -6)\)を図に入れて確かめてみましょう。
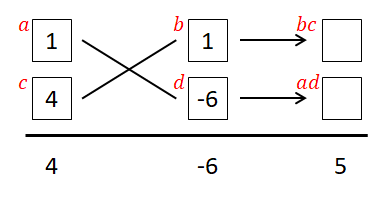
図の右側も埋めましょう。 右上は\(bc = 4\),右下は\(ad = -6\)です。
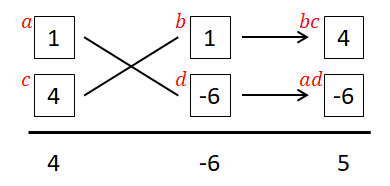
図を埋めたところ\(ad + bc = -6 + 4 = -2\)になりましたね。 残念ながら\(5\)にならなかったのでこの組み合わせは失敗です。
\(b\)と\(d\)を入れ換えたパターンも確認しましょう。 図を埋めると次のようになります。
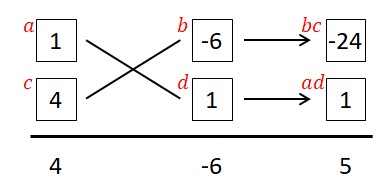
\(ad + bc = -23\)です。これもダメですね。 どうやら\((1, -6)\)はハズレだったようです。
\(a, d\)の入れ換えは確認しなくても良いですが\(b, d\)の入れ換えは確認必須です。 上の例を見ても\(b, d\)の入れ換えで違う結果になるのが分かります。
\((-1, 6)\)の組み合わせもダメです。(確かめてみてください。) 次は\((2, -3)\)の組み合わせを試します。 図を埋めてみましょう。
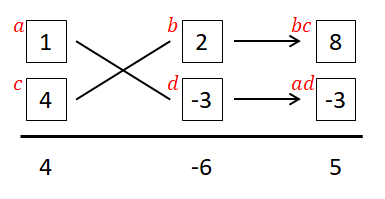
\(ad + bc = 5\)です。アタリですね! というわけで\(4x^2 + 5x - 6 = (x + 2)(4x - 3)\)と因数分解できることが分かりました。 図の\(a, b, c, d\)を\((ax + b)(cx + d)\)に当てはめたわけです。
これがたすき掛けの流れです。長かったですね。 確認問題も解いてみて慣れておきましょう。
確認問題
次の整式を因数分解してください。
-
\(x^2 + 10x + 25\)
-
\(4x^2 - 12x + 9\)
-
\(9x^2 - 1\)
-
\(x^2 + 17x + 16\)
-
\(x^2 - 4x - 32\)
答え
-
平方の形へ因数分解できます。
\( \begin{align} &x^2 + 10x + 25 \\[5pt] &= x^2 + 2 \cdot x \cdot 5 + 5^2 \\[5pt] &= \textcolor{red}{(x + 5)^2} \end{align} \) -
平方の形へ因数分解できます。
\( \begin{align} &4x^2 - 12x + 9 \\[5pt] &= (2x)^2 - 2 \cdot (2x) \cdot 3 + 3^2 \\[5pt] &= \textcolor{red}{(2x - 3)^2} \end{align} \) -
和と差の積へ因数分解できます。
\( \begin{align} &9x^2 - 1 \\[5pt] &= (3x)^2 - 1^2 \\[5pt] &= \textcolor{red}{(3x + 1)(3x - 1)} \end{align} \) -
1次式の積へ因数分解できます。
\( \begin{align} &x^2 + 17x + 16 \\[5pt] &= x^2 + (1 + 16)x + 1 \cdot 16 \\[5pt] &= \textcolor{red}{(x + 1)(x + 16)} \end{align} \) -
1次式の積へ因数分解できます。
\( \begin{align} &x^2 - 4x - 32 \\[5pt] &= x^2 + (-8 + 4)x + (-8) \cdot 4 \\[5pt] &= \textcolor{red}{(x - 8)(x + 4)} \end{align} \)
次の整式を因数分解してください。
-
\(x^2 + x + \displaystyle\frac{1}{4}\)
-
\(x^3y + 8x^2y^2 + 7xy^3\)
答え
-
係数がすべて整数になるように計算すると分かりやすいです。
\( \begin{align} &x^2 + x + \frac{1}{4} \\[5pt] &= \frac{1}{4}(4x^2 + 4x + 1) \\[5pt] &= \frac{1}{4}\{(2x)^2 + 2 \cdot (2x) \cdot 1 + 1^2\} \\[5pt] &= \textcolor{red}{\frac{1}{4}(2x + 1)^2} \end{align} \)次のように分数のまま扱うのもアリです。
\( \begin{align} &x^2 + x + \frac{1}{4} \\[5pt] &= x^2 + 2 \cdot x \cdot \frac{1}{2} + \left(\frac{1}{2}\right)^2 \\[5pt] &= \textcolor{red}{\left(x + \frac{1}{2}\right)^2} \end{align} \) -
共通因数があれば,まずは共通因数でくくりましょう。
\( \begin{align} &x^3y + 8x^2y^2 + 7xy^3 \\[5pt] &= xy(x^2 + 8xy + 7y^2) \\[5pt] &= xy\{x^2 + (y + 7y)x + y \cdot (7y)\} \\[5pt] &= \textcolor{red}{xy(x + y)(x + 7y)} \end{align} \)
次の整式を因数分解してください。
-
\(2x^2 + 11x + 5\)
-
\(6x^2 + 13x + 6\)
-
\(2x^2 + xy - 3y^2\)
-
\(8x^2 - 2xy - 3y^2\)
答え
-
たすき掛けの練習です。
\( 2x^2 + 11x + 5 = \textcolor{red}{(x + 5)(2x + 1)} \)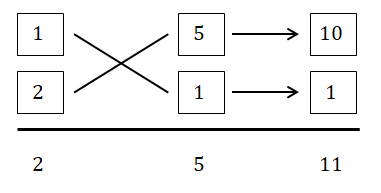
-
たすき掛けの練習です。
\( 6x^2 + 13x + 6 = \textcolor{red}{(2x + 3)(3x + 2)} \)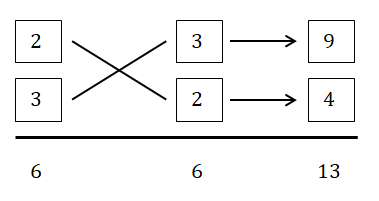
-
たすき掛けの練習です。
\( 2x^2 + xy - 3y^2 = \textcolor{red}{(x - y)(2x + 3y)} \)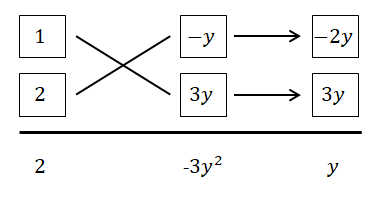
-
たすき掛けの練習です。
\( 8x^2 - 2xy - 3y^2 = \textcolor{red}{(2x + y)(4x - 3y)} \)