これまで\(1, -3, \displaystyle\frac{1}{4}\)のような数(有理数)を扱ってきました。 ここでは扱う数の範囲を「実数」まで拡張していきます。
目次
整数
小学校の算数から色々な数を学んできました。 まず初めに出会う数は自然数(\(1, 2, 3, \cdots\))です。 ふだん数を数えたりするのに使う数ですね。 \(0\)は自然数に含めないことも忘れないでください。
大学からの数学では\(0\)を自然数に含めることもあります。 流儀や利便性次第で自然数だったり自然数でなかったりします。 \(0\)を自然数に含めるべきかという議論にはあまり意味がありません。
ただ高校までの数学では\(0\)を自然数に含めないと決めているだけです。 なぜ自然数じゃないんだ...なんて深く考えなくても良いですよ。
自然数に「ゼロ」と「マイナス」の概念を追加することで整数ができます。 「ゼロ」は「何もない」を,「マイナス」は「不足」を表現できます。
\(0\)より大きい整数を正の整数,\(0\)より小さい整数を負の整数と呼びます。 正の整数はちょうど自然数と一致しますね。
「\(0\)より大きい」を正,「\(0\)より小さい」を負といいますが,非負という言葉もよく使います。 非負は,文字通り「負でない」という意味なので,「\(0\)以上」を指します。
有理数
整数だけでは表現できない数がまだまだあります。 大きさが\(1\)のケーキを\(4\)等分したらそれぞれのケーキの大きさはいくつでしょうか。 \(1\)よりも小さく\(0\)よりも大きいサイズになることは想像できます。 つまり\(0\)と\(1\)の間にもまだ数が存在するわけです。
この大きさを\(\displaystyle\frac{1}{4}\)と表現します。 これは\(4\)つに分けた内の\(1\)つという「比」による表現法で分数といいます。 このように整数をうまく組み合わせることで新しい数を表現できるわけです。
分数は小数に書き換えることができます。 \(\displaystyle\frac{1}{4} = 0.25\)ですね。 このような無限に続かない小数を有限小数といいます。
\(\displaystyle\frac{1}{3} = 0.333 \cdots\)のように無限に続く小数は無限小数といいます。 特にこの例のように同じ数字の列がループするものは循環小数といいます。 ループする数字の上に・をつけて\(0.\dot{3}\)と表すこともあります。 \(0.203203 \cdots\)というループなら\(0.\dot{2}0\dot{3}\)と表します。
ここまでで説明した整数,有限小数,循環小数をまとめて有理数といいます。 有理数の重要な特徴は必ず2つの整数の比で表現できることです。 言い換えれば,有理数とは2つの整数\(m, n\)を用いて\(\displaystyle\frac{n}{m}\)と表せる数です。
無理数
先ほど無限小数の説明をしました。 無限小数の例に出した\(\displaystyle\frac{1}{3} = 0.\dot{3}\)は循環小数でした。 では循環しない無限小数というものはあるのでしょうか。
答えは,あります。 有理数だけでは表現できない数はまだあるのです。 そのような数(循環しない無限小数)を無理数といいます。
無理数の例は\(\sqrt{2}, \sqrt{5}, \pi\)などです。 それぞれ\(1.414\cdots,\ 2.236\cdots,\ 3.141\cdots\)のように循環しない無限小数ですね。
無理数は日常であまり使わない印象があり少し難しそうですね。 かの有名なピタゴラスも無理数の存在を否定しました。 無理数を発見した弟子を殺してしまったという逸話さえあります。
そんな無理数も実はありふれた数です。 紙の寸法(黄金比)や円の面積など身の回りには多くの無理数があります。 (とはいえ日常で無理数を意識することは滅多にないですが。。。)
実数
ここまでで説明した有理数と無理数を合わせて実数といいます。 実数があれば物の個数や長さ,重さなど日常でよく使う量が全て表せます。
色んな種類の数が出てきたので一度絵に書いて整理しておきます。 それぞれの種類の数の例を〇で囲って示してあります。
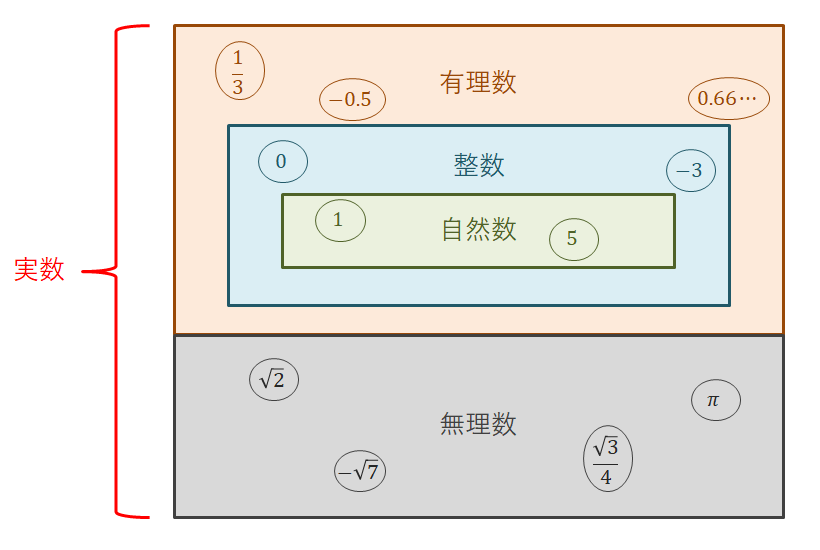
高校数学では使われませんが,数の集合を表す一般的な記号を紹介しておきます。 集合については,また後で学びます。
自然数全体の集合を\(\mathbb{N}\)で表します。 英語で Natural number というからです。
整数全体の集合を\(\mathbb{Z}\)で表します。 ドイツ語で数を意味する Zahlen に由来します。
有理数全体の集合を\(\mathbb{Q}\)で表します。 イタリア語で商を意味する Quoziente に由来します。
実数全体の集合を\(\mathbb{R}\)で表します。 英語で Real number というからです。
無理数全体の集合を表す一般的な記号はありません。 無理数は実数のうち,有理数でないものなので,\(\mathbb{R} \setminus \mathbb{Q}\)や\(\mathbb{R} - \mathbb{Q}\)で表します。 \(\mathbb{R}\)から\(\mathbb{Q}\)にもあるものを除く,という意味です。
また,数学Ⅱで学びますが,複素数という数もあります。 複素数全体の集合は\(\mathbb{C}\)で表します。 英語で Complex number というからです。
数直線
実数を簡単な絵で表現して扱いやすくする方法を身につけましょう。 すべての実数の間には大小関係がありますし,一列に並べることができそうですね。
実数を一列に並べるためにはまず並べる場所である「直線」が必要です。 それと「\(0\)の位置」「\(1\)の大きさ」を決めておく必要があります。 これを描いたのが下図です。
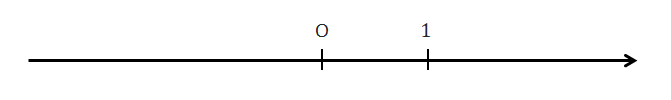
「直線」は実数の大小関係を表現できるように矢印にしておきます。 「\(0\)の位置」はO(オー)で表していて,原点といいます。 「\(1\)の長さ」はOと\(1\)の間の長さです。
これですべての実数を直線上に並べる準備ができました。 右に向かってだんだん大きくなるように実数を並べれば,数直線のできあがりです。 試しに整数を並べてみると下図のようになります。
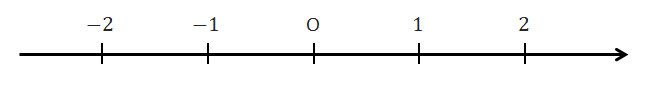
実際には整数以外にも無数の実数がありますが,普通は必要な数だけ書いて利用します。 そのあたりの感覚は今後使いながら覚えていきましょう。
ここまで数や数直線についてざっくり説明しました。 ざっくり過ぎてすっきりしない場合は,解析学の入門書などを手にとってみましょう。
最後にいくつかの用語を説明しておきます。 実数\(x\)が数直線上の点\(P\)に対応しているとき,\(x\)を\(P\)の座標といいます。 またこの点\(P\)と原点Oとの間の距離を実数\(x\)の絶対値といいます。 次回は絶対値の計算を練習します。
確認問題
-
次の5つの数の内,自然数はどれか,すべて答えて下さい。
\( 50, \ \ 0, \ \ \displaystyle\frac{2}{3}, \ \ -1, \ \ 0.5 \) -
次の5つの数の内,整数はどれか,すべて答えて下さい。
\( 50, \ \ 0, \ \ \displaystyle\frac{2}{3}, \ \ -1, \ \ 0.5 \) -
次の5つの数の内,有理数はどれか,すべて答えて下さい。
\( 0, \ \ -\displaystyle\frac{7}{5}, \ \ \sqrt{15}, \ \ \pi + 2, \ \ \displaystyle\frac{1}{\sqrt{5}} \) -
次の5つの数の内,無理数はどれか,すべて答えて下さい。
\( 0, \ \ -\displaystyle\frac{7}{5}, \ \ \sqrt{15}, \ \ \pi + 2, \ \ \displaystyle\frac{1}{\sqrt{5}} \) -
次の5つの数の内,実数はどれか,すべて答えて下さい。
\( 0, \ \ -\displaystyle\frac{7}{5}, \ \ \sqrt{15}, \ \ \pi + 2, \ \ \displaystyle\frac{1}{\sqrt{5}} \)
答え
-
\(50\)
-
\(50, \ \ 0, \ \ -1\)
-
\(0, \ \ -\displaystyle\frac{7}{5}\)
-
\(\sqrt{15}, \ \ \pi + 2, \ \ \displaystyle\frac{1}{\sqrt{5}}\)
-
\(0, \ \ -\displaystyle\frac{7}{5}, \ \ \sqrt{15}, \ \ \pi + 2, \ \ \displaystyle\frac{1}{\sqrt{5}}\)
循環小数と分数の問題です。
-
\(\displaystyle\frac{1}{6}\)を循環小数で表してください。
-
\(x = 0.\dot{1}\dot{2}\)とします。 \(100x - x\)を計算して\(x\)を分数で表してください。
-
(2)を参考にして\(0.1\dot{2}\dot{3}\)を分数で表してください。
答え
-
単純に割り算すると\(\displaystyle\frac{1}{6} = 0.16666\cdots\)となるので,\(\displaystyle\frac{1}{6} = \textcolor{red}{0.1\dot{6}}\)です。
-
\(x = 0.1212\cdots\)なので,\(100x = 12.1212\cdots\)です。 よく見ると両者の小数部分は全く同じですから,\(100x - x = 12\)です。 つまり\(99x = 12\)なので,\(x = \displaystyle\frac{12}{99} = \textcolor{red}{\displaystyle\frac{4}{33}}\)です。
-
(2)から循環小数は,循環部分をうまく打ち消せば分数に直せることが分かりました。 (2)と同じように\(x = 0.1\dot{2}\dot{3} = 0.1232323\cdots\)としましょう。 今回は\(2323\cdots\)という循環をうまく打ち消せば良いわけです。 循環部分の始まりから小数部分が始まるように調整してみましょう。
\(10x = 1.2323\cdots\),\(1000x = 123.2323\cdots\)なので, \(1000x - 10x = 122\)となり,\(x = \displaystyle\frac{122}{990} = \textcolor{red}{\displaystyle\frac{61}{495}}\)です。
実数\(x\)が整数\(a\)と小数\(b \ (0 \leqq b \lt 1)\)を用いて\(x = a + b\)と表せるとき, \(a\)を実数\(x\)の整数部分,\(b\)を実数\(x\)の小数部分といいます。
例えば\(2.12\)は\(2.12 = 2 + 0.12\)と表せるので,整数部分は\(2\)で小数部分は\(0.12\)です。 小数部分は\(0\)以上\(1\)未満であることに注意してください。
ちなみに無理数の小数部分を直接小数で表すことはできません。 例えば\(\sqrt{2}\)の整数部分は\(1\)ですが,小数部分は\(\sqrt{2} - 1\)と表すしかありません。
-
\(12.77\)の整数部分・小数部分を答えてください。
-
\(-12.77\)の整数部分・小数部分を答えてください。
-
\(\sqrt{5}\)の整数部分・小数部分を答えてください。
-
\(\pi + 5\)の整数部分・小数部分を答えてください。
答え
-
整数部分は\(12\),小数部分は\(0.77\)です。
-
整数部分は\(-12\),小数部分は\(0.77\)! …としたいところですが,残念ながら違います。\(-12 + 0.77 \neq -12.77\)ですね。 じゃあ小数部分は\(-0.77\)だ!と思うかもしれませんが,小数部分は\(0\)以上\(1\)未満なのでダメです。
正解は,整数部分は\(-13\),小数部分は\(0.23\)です。 実は\(x\)の整数部分\(a\)は「\(x\)を超えない最大の整数」になります。 残りの小数部分\(b\)は\(b = x - a\)で求められます。
-
\(\sqrt{5} = 2.236\cdots\)なので整数部分は\(2\),小数部分は\(\sqrt{5} - 2\)です。 無理数の小数部分は直接小数で表せないんでしたね。
-
\(\pi = 3.141\cdots\)なので\(\pi + 5 = 8.141\cdots\)です。 よって整数部分は\(8\),小数部分は\(\pi - 3\)です。 これも無理数なので小数部分を直接小数で表すことはできません。
