場合の数の中でも,特に「並べ方」や「選び方」を考えることは基本です。 今回は「並べ方」である順列を考えます。
目次
順列
いくつかのものに順序をつけて\(1\)列に並べたものを順列といいます。 その並べ方の総数を考えていきましょう。
\(3\)つの箱\(A\),\(B\),\(C\)を\(1\)列に並べるとき,その並べ方は何通りあるでしょうか? 樹形図をかいてみると,次のようになります。
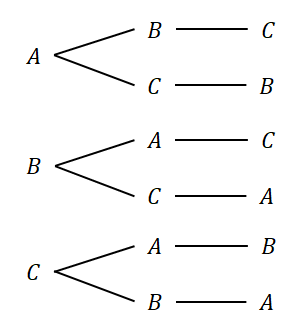
樹形図を左から順に見ると分かる通り,\(1\)つめの選び方は\(3\)通りありますが,\(2\)つめの選び方はそれぞれ\(2\)通りずつしかなく,\(3\)つめは残りの\(1\)つしか選びようがありません。 したがって,並べ方の総数は次のように計算できます。
これは\(3\)個のものの並べ方に限った話ではありません。 \(n\)個のものを並べるときも,\(1\)つめの選び方は\(n\)通り,\(2\)つめはそれ以外から選ぶので\(n - 1\)通り,…というように選び方が決まってきますから,次が成り立ちます。
異なる\(n\)個のものを\(1\)列に並べるとき,並べ方の総数は次の計算で求められる。
これを\(n!\)と書き,\(n\)の階乗と読む。 ただし,\(0! = 1\)とする。
\(0! = 1\)とするのは気持ち悪いかもしれません。 その理由は色々な意味で都合が良いからですが,ひとまずは次の考え方が理解しやすいと思います。
\(n!\)について,\(n \geqq 2\)の範囲で次が成り立つことが分かりますね。
ここで\(n = 1\)としてみると,次のようになります。
つまり\(0! = 1\)としておけば,上の関係式が\(n = 1\)のときも成り立つことになります。 \(0! = 1\)とするのが統一感のある定義になるのです。
同様に\(n\)個から\(r\)個を取り出して\(1\)列に並べる順列も考えられます。 これも先ほどと同じく\(1\)つめの選び方は\(n\)通り,\(2\)つめの選び方は\(n - 1\)通り,…となります。
先ほどとの違いは,\(r\)個しか並べないことですから,並べ方の総数は次のように求められます。 先ほどの計算を\(r\)個の積で打ち切った形ですね。
異なる\(n\)個のものから\(r\)個を取り出して\(1\)列に並べるとき,並べ方の総数は次の計算で求められる。
これを\({}_n\mathrm{P}_r\)と書く。
\(\mathrm{P}\)は順列を英語で表した Permutation から来ています。 式だけ見るとややこしいかもしれませんが,\(n\)から\(1\)ずつ減らした数の\(r\)個の積ですね。 次の計算例を確認しておきましょう。
意味を考えれば当たり前の式ですから,暗記よりも理解が大事です!
グループを含む順列
\(1\)と書かれたカードが\(1\)枚,\(2\)と書かれたカードが\(2\)枚,\(3\)と書かれたカードが\(3\)枚あります。 ただしそれぞれのカードは,同じ数字が書かれたものでも区別可能であるとします。 このカードを\(1\)列に並べる方法の総数を考えてみましょう。
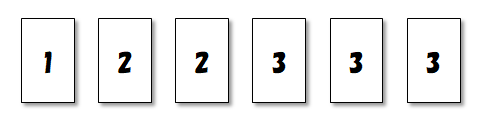
ただ単に並べるだけなら,カードに書かれた数字は関係ありません。 ただ\(6\)枚のカードを並べるだけですから,並べ方の総数は次の通りです。
では,「\(2\)のカード\(2\)枚を必ず隣同士にする」という条件を付けたらどうでしょう。 先ほどの公式を当てはめるだけではダメそうですね。
\(2\)のカードが隣り合うようにした並べ方の例を見てみましょう。 隣接したものたちは,常に\(1\)つのグループを成していると考えると良いです。
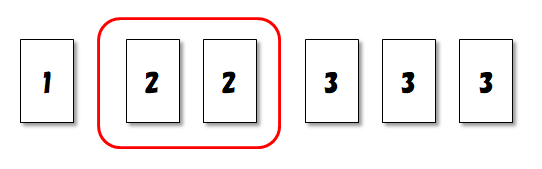
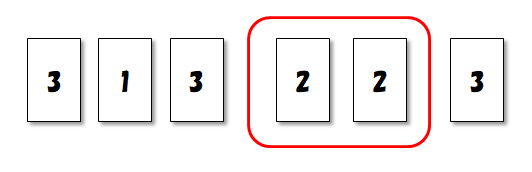
このようにグループ化して考えると,\(4\)枚のカードと\(1\)つのグループを並べる方法を数えれば良いことが分かります。 この合計\(5\)つのものの並べ方は\(5!\)通りですね。
さらにグループ内のカードの並べ方が\(2!\)通りありますから,結局条件を満たす並べ方の総数は次の通りになります。
グループ化する発想はよく使うので,慣れておきましょう。
辞書順と順列
ここまでは単純に順列が何通りあるかを考えてきました。 次は順列に順序をつけて考えてみましょう。
例えば数字の順列であれば,数の大きさで順序が決まりますし,アルファベットの順列であれば,辞書式順序があります。 ここでは辞書式順序をもつ順列の例を見てみましょう。
次のアルファベットを\(1\)列に並べて文字列を作ります。
文字列は全部で\(5! = 120\)通りあります。 \(\mathrm{STUDY}\)という文字列が辞書順で何番目にくるのか考えてみましょう。 考えやすいように,まずはこれをアルファベット順に並べ直しておきます。
\(\mathrm{STUDY}\)が何番目にくるか,一発の計算で求めることはできません。 本物の辞書で\(\mathrm{STUDY}\)を調べるとき,まず\(\mathrm{S}\)で始まるページを開いて,その中で\(\mathrm{T}\)で始まるところを探して,…というように先頭の文字から順に確定していきますよね。 この問題も同じ考え方です。
まず\(\mathrm{S}\)で始まる文字列が何番目から始まるかを考えましょう。 \(\mathrm{S}\)で始まる文字列は,\(\mathrm{D}\)で始まる文字列が出尽くした後に出てきますね。 ですからまずは\(\mathrm{D}\)で始まる文字列を全て数えます。
この形の文字列は,残り\(4\)文字の順列の数だけあるのですから,\(\mathrm{D}\)で始まる文字列は次の数だけあります。
というわけで,\(\mathrm{S}\)で始まる文字列は\(25\)番目から始まるようです。 次は\(\mathrm{ST}\)で始まる文字列の開始点を考えます。 \(\mathrm{ST}\)で始まる文字列の手前には\(\mathrm{SD}\)で始まる文字列がありますから,まずこれを数えます。
この形の文字列は,残り\(3\)文字の順列の数だけあるのですから,\(\mathrm{SD}\)で始まる文字列は次の数だけあります。
ここまで絞り込めばあとちょっとですから,あとは実際に文字列を辞書順で書き出して確認してみましょう。
これで\(\mathrm{STUDY}\)が\(33\)番目の文字列だということが分かりました。 まずは計算で大体の位置を把握して,最後は具体的に書き出してやれば良いですね。
確認問題
次の数字から異なる\(3\)個を取り出して並べ,\(3\)桁の整数を作ります。 ただし\(021\)のように先頭が\(0\)になってはいけません。
次の問いに答えてください。
-
何通りの整数ができるか答えてください。
-
何通りの偶数ができるか答えてください。
答え
先頭の数字が\(0\)になってはならないことに注意しましょう。
-
先頭の数字は\(0\)でないものですから,\(4\)通りしかありえません。 後の\(2\)桁は残り\(4\)個の数字のどれを使っても良いので,その順列は\({}_4 \mathrm{P}_2\)通りです。 したがって,次の数だけ整数を作ることができます。
\( \begin{align} 4 \times {}_4 \mathrm{P}_2 &= 4 \times 4 \times 3 \\[5pt] &= 48 \end{align} \)というわけで,整数は\(48\)通りできます。
-
問題の数字から偶数を作るには,一の位を\(0\)か\(2\)にするしかありません。 それぞれの場合について考えてみましょう。
[1] まずは一の位が\(0\)の場合を考えます。
\( \begin{align} \Box\Box 0 \end{align} \)この場合,先頭に\(0\)が来ることはもうありませんから,先頭\(2\)つの数字は自由に並べてOKです。 その並べ方は次の数だけありますね。
\( \begin{align} {}_4 \mathrm{P}_2 &= 4 \times 3 \\[5pt] &= 12 \end{align} \)[2] 次に一の位が\(2\)の場合を考えます。
\( \begin{align} \Box\Box 2 \end{align} \)この場合,先頭に\(0\)が来ないように注意する必要があります。 先頭は\(0\)と\(2\)以外から選ぶので,その選び方は\(3\)通りです。 \(2\)桁目は残り\(3\)個の数字のどれが来てもOKですから,このような偶数は次の数だけあります。
\( \begin{align} 3 \times 3 = 9 \end{align} \)以上から,偶数は\(12 + 9 = \)\(21\)通りできます。
千葉県民\(2\)人,大阪府民\(3\)人,福岡県民\(2\)人に\(1\)列に並んでもらいます。 次の問いに答えてください。
-
並び方が全部で何通りあるか答えてください。
-
千葉県民が隣り合わない並び方が何通りあるか答えてください。
-
両端とちょうど真ん中に大阪府民がくる並び方が何通りあるか答えてください。
答え
隣り合うものはグルーピングすると考えやすいです。
-
合計\(7\)人の並び方を考えるだけですから,並び方の数は次のように計算できます。
\( \begin{align} 7! &= 7 \cdot 6 \cdots 2 \cdot 1 \\[5pt] &= 5040 \end{align} \)というわけで,並び方の総数は\(5040\)通りあります。
-
隣り合わない状況を考えるよりも,隣り合う状況を考える方が簡単です。 まず千葉県民が隣り合う並び方を考えます。
千葉県民は常に隣同士なのですから,この\(2\)人は\(1\)つのグループとして考えます。 そうすると,他\(5\)人の人と\(1\)つのグループの並べ方を考えれば良いことになります。 その並べ方は\(6!\)通りあります。
また,グループ内での並べ方も\(2!\)通りのパターンがありますから,千葉県民が隣り合う並び方は次の数だけあります。
\( \begin{align} 6! \times 2! &= 720 \times 2 \\[5pt] &= 1440 \end{align} \)したがって,千葉県民が隣り合わない並び方は,\(5040 - 1440 = \)\(3600\)通りあります。
-
大阪府民の並ぶ位置は決まっていますから,大阪府民の並び方は\(3\)人の並び方の総数である\(3!\)通りしかありません。
また,他の\(4\)人は大阪府民のいない位置に自由に並べられるので,その並べ方は\(4!\)通りあります。
したがって,題意の並べ方は次の計算で求められます。
\( \begin{align} 3! \times 4! &= 6 \times 24 \\[5pt] &= 144 \end{align} \)というわけで,題意の並べ方は\(144\)通りあります。
次のアルファベットから異なる\(4\)個を選んで\(1\)列に並べ,文字列を作ります。
できた文字列を辞書順に並べるとき,次の問いに答えてください。
-
できる文字列が全部で何通りあるか答えてください。
-
\(\mathrm{CAFE}\)が何番目にあるか答えてください。
-
\(270\)番目の文字列を答えてください。
答え
辞書順の考え方は,本物の辞書を引くときと一緒です。 先頭の文字から順に確定させていくようにすると,うまく数えられます。
-
\(6\)文字の内\(4\)文字を並べる方法ですから,その並べ方の総数は次の計算で求められます。
\( \begin{align} {}_6 \mathrm{P}_4 &= 6 \cdot 5 \cdot 4 \cdot 3 \\[5pt] &= 360 \end{align} \)というわけで,答えは\(360\)通りです。
-
先頭の文字から順に確定させていきましょう。 まず\(\mathrm{C}\)で始まる文字列が何番目から始まるかを考えます。
\(\mathrm{C}\)で始まる文字列は,\(\mathrm{A}\)で始まる文字列と\(\mathrm{B}\)で始まる文字列の次にきます。 先にこれらの個数を数えましょう。
\( \begin{align} &\mathrm{A}\Box\Box\Box \\[5pt] &\mathrm{B}\Box\Box\Box \\[5pt] &\mathrm{C}\Box\Box\Box \end{align} \)\(\mathrm{A}\)で始まる文字列は,\(\mathrm{A}\)の後に\(3\)文字が続きます。 その\(3\)文字は,\(\mathrm{A}\)以外の\(5\)文字から選べますから,その総数は次の計算で求められます。
\( \begin{align} {}_5 \mathrm{P}_3 &= 5 \cdot 4 \cdot 3 \\[5pt] &= 60 \end{align} \)同様に\(\mathrm{B}\)で始まる文字列も\(60\)個あります。 これで\(\mathrm{C}\)で始まる文字列は\(121\)番目から始まることが分かりました。
\( \begin{align} &\mathrm{A}\Box\Box\Box \implies 1 \sim 60 \\[5pt] &\mathrm{B}\Box\Box\Box \implies 61 \sim 120 \\[5pt] &\mathrm{C}\Box\Box\Box \implies 121 \sim \end{align} \)\(\mathrm{C}\)で始まる文字列は,まず\(\mathrm{CA}\)で始まるものから現れますから,\(\mathrm{CA}\)で始まる文字列も\(121\)番目から始まりますね。
\( \begin{align} &\mathrm{A}\Box\Box\Box \implies 1 \sim 60 \\[5pt] &\mathrm{B}\Box\Box\Box \implies 61 \sim 120 \\[5pt] &\mathrm{CA}\Box\Box \implies 121 \sim \end{align} \)続いて\(\mathrm{CAF}\)で始まる文字列が何番目から始まるか考えます。 その前に\(\mathrm{CAB}\),\(\mathrm{CAD}\),\(\mathrm{CAE}\)で始まる文字列がありますね。 これらの文字列は,最後の\(1\)文字が未使用の\(3\)文字から選べるので,それぞれ\(3\)通りあります。
\( \begin{align} &\mathrm{A}\Box\Box\Box \implies 1 \sim 60 \\[5pt] &\mathrm{B}\Box\Box\Box \implies 61 \sim 120 \\[5pt] &\mathrm{CAB}\Box \implies 121 \sim 123 \\[5pt] &\mathrm{CAD}\Box \implies 124 \sim 126 \\[5pt] &\mathrm{CAE}\Box \implies 127 \sim 129 \\[5pt] &\mathrm{CAF}\Box \implies 130 \sim \end{align} \)あとは順番に書き出してしまいましょう。
\( \begin{align} &\mathrm{A}\Box\Box\Box \implies 1 \sim 60 \\[5pt] &\mathrm{B}\Box\Box\Box \implies 61 \sim 120 \\[5pt] &\mathrm{CAB}\Box \implies 121 \sim 123 \\[5pt] &\mathrm{CAD}\Box \implies 124 \sim 126 \\[5pt] &\mathrm{CAE}\Box \implies 127 \sim 129 \\[5pt] &\mathrm{CAFB} \implies 130 \\[5pt] &\mathrm{CAFD} \implies 131 \\[5pt] &\mathrm{CAFE} \implies 132 \end{align} \)これで\(\mathrm{CAFE}\)が\(132\)番目の文字列であることが分かりました。
-
順番に文字列を\(270\)個並べてみるわけにもいかないので,ざっくり数えて少しずつ見当をつけていきましょう。
まずは\(1\)文字目を決めたいと思います。 (2)でも見た通り,\(\mathrm{A}\)で始まる文字列は\(60\)個あります。 同様に\(\mathrm{B}\)や\(\mathrm{C}\)で始まる文字列もそれぞれ\(60\)個ずつありますね。
\( \begin{align} &\mathrm{A}\Box\Box\Box \implies 1 \sim 60 \\[5pt] &\mathrm{B}\Box\Box\Box \implies 61 \sim 120 \\[5pt] &\mathrm{C}\Box\Box\Box \implies 121 \sim 180 \\[5pt] &\mathrm{D}\Box\Box\Box \implies 181 \sim 240 \\[5pt] &\mathrm{E}\Box\Box\Box \implies 241 \sim 300 \\[5pt] &\mathrm{F}\Box\Box\Box \implies 301 \sim 360 \end{align} \)こうしてざっくり数えてみると,\(270\)番目の文字列は\(\mathrm{E}\)で始まることが分かりますね。
次に\(2\)文字目を決めるために,\(\mathrm{EA}\)や\(\mathrm{EB}\)で始まる文字列を考えます。 これらの文字列の後には,未使用の\(4\)文字から選んだ\(2\)文字が並びますから,それぞれの文字列は\({}_4 \mathrm{P}_2 = 12\)個だけありますね。
\( \begin{align} &\mathrm{EA}\Box\Box \implies 241 \sim 252 \\[5pt] &\mathrm{EB}\Box\Box \implies 253 \sim 264 \\[5pt] &\mathrm{EC}\Box\Box \implies 265 \sim 276 \\[5pt] &\mathrm{ED}\Box\Box \implies 277 \sim 288 \\[5pt] &\mathrm{EF}\Box\Box \implies 289 \sim 300 \end{align} \)これで\(270\)番目の文字列は\(\mathrm{EC}\)で始まることが分かりましたね。
あとちょっとなので,\(\mathrm{EC}\)から始まる文字列を順番に書き出して\(270\)番目のものを見つけてしまいましょう。
\( \begin{align} &\mathrm{ECAB} \implies 265 \\[5pt] &\mathrm{ECAD} \implies 266 \\[5pt] &\mathrm{ECAF} \implies 267 \\[5pt] &\mathrm{ECBA} \implies 268 \\[5pt] &\mathrm{ECBD} \implies 269 \\[5pt] &\mathrm{ECBF} \implies 270 \\[5pt] &\mathrm{ECDA} \implies 271 \\[5pt] &\mathrm{ECDB} \implies 272 \\[5pt] &\mathrm{ECDF} \implies 273 \\[5pt] &\mathrm{ECFA} \implies 274 \\[5pt] &\mathrm{ECFB} \implies 275 \\[5pt] &\mathrm{ECFD} \implies 276 \end{align} \)これで\(270\)番目の文字列が\(\mathrm{ECBF}\)であることが分かりました。
