前回\(1\)列に並べる順列を学びましたが,ものの並べ方は\(1\)列にする以外にも色々あります。 今回は円形の並べ方を考えてみます。
目次
円順列
席を\(5\)つ用意して,\(5\)人を座らせるとき,その並び方は何通りあるでしょうか? \(5\)人の人には\(1\)から\(5\)の番号を付けます。
席が\(1\)列に並んでいる場合は,並び方の総数は次の計算で求められますね。
では席が円形に並んでいる場合はどうでしょうか? それぞれの席を座標などで明確に区別した"座り方"であれば,\(1\)列に並べる場合と同じく\(120\)通りです。 下の\(2\)つの座り方を区別する場合ですね。
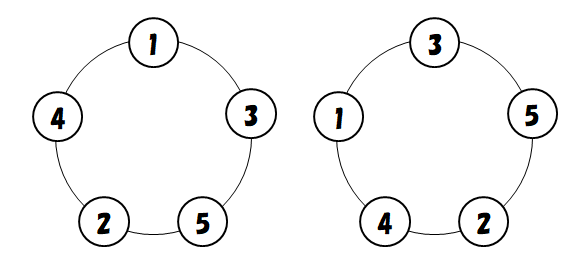
しかしこの\(2\)つの座り方は,少し回転するだけで完全に一致します。 つまり座った人の並び順自体は同じなのです。 "座り方"は\(120\)通りあっても,"並び方"は明らかにそんなにないですね。
いくつかのものを円形に並べたものを円順列といいますが,この"並び方"はまさに円順列の問題です。 その"並び方"の総数をどうやって求めたら良いでしょうか?
ひとつの考え方として,重複して数えた分を排除する方法があります。 上の円順列では,ひとつの並び方につき,座り方が下図のように\(5\)パターンありますね。 これらは少し回転すれば全て一致する並び方です。
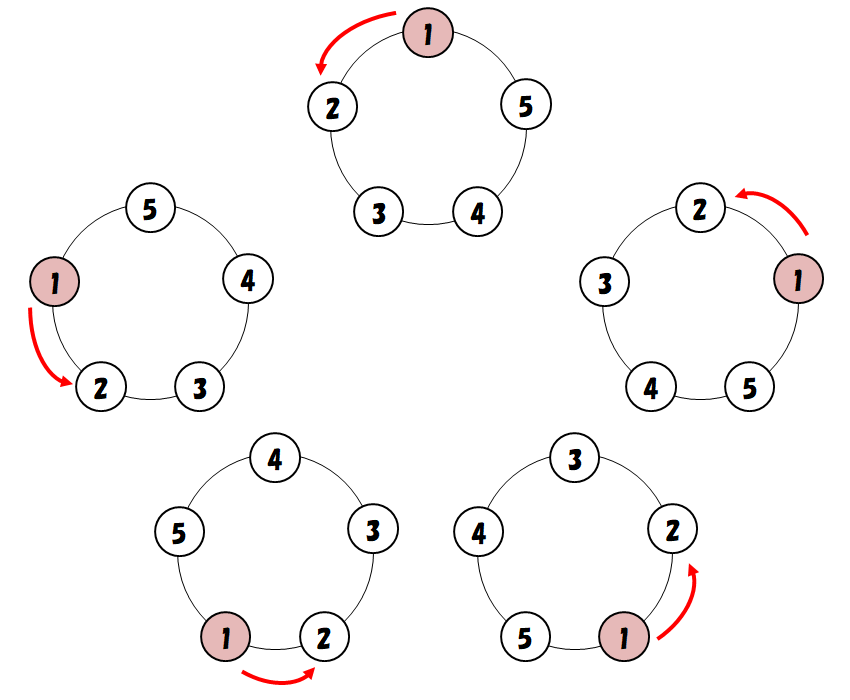
ということは,初めに求めた座り方の\(5! = 120\)通りは,並び方の\(5\)倍の数になっているわけです。 同じ並び方を\(5\)回ずつ数えていたわけですからね。
つまり,この円順列の並び方は次の数だけあることが分かります。
ざっくり数えてから,重複して数えた分を調整する方法ですね。 よく使う考え方なので,慣れておきましょう。
もうひとつの考え方として,\(1\)箇所を固定してしまう方法があります。 円順列の中のどこかには,必ず\(1\)番の人がいますが,その位置を下図のように一番上の席に固定してしまうのです。
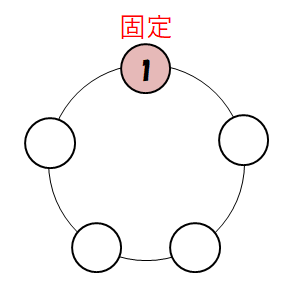
先ほども見たように,ひとつの並び方につき,座り方は\(5\)パターンあります。 これらは全て同じ並び方なのですから,わざわざ\(5\)回重複して数える必要はありませんね。
並び方が同じ\(5\)パターンの中には,\(1\)番の人が一番上の席にいる場合が\(1\)つあります。 この場合のみを数えることにすれば,同じ並び方を重複して数えずに済みます。
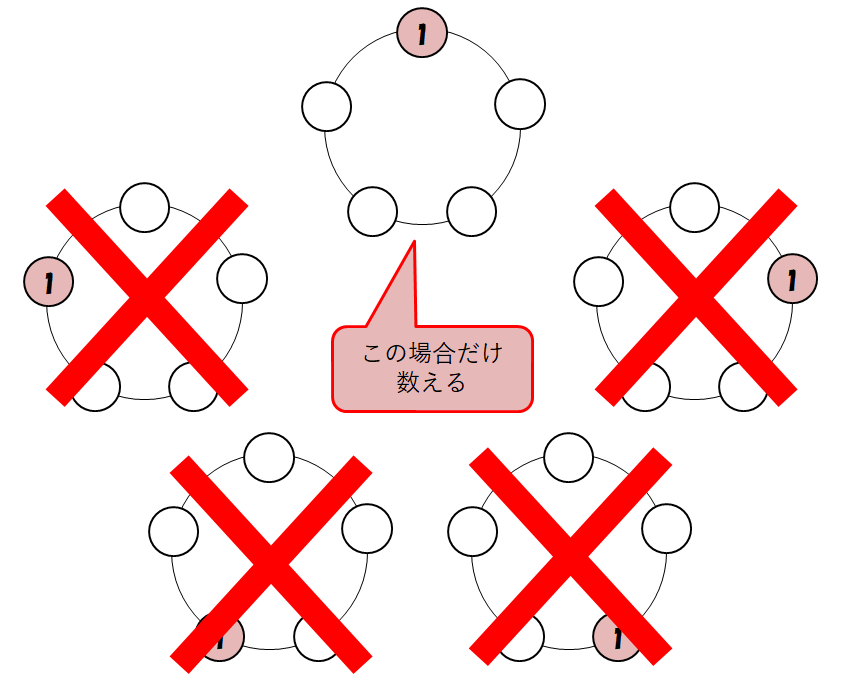
これが\(1\)番の人の位置を固定するということの意味です。 重複して数えないための工夫なのです。 実際には\(1\)番の人が一番上の席に座るとは限りませんが,そんなことは関係ありません。
さて,こう考えれば並び方を数えるのは簡単です。 残った\(4\)つの席に\(4\)人を並べるだけですから,その並べ方は次の数だけあります。
このように特定箇所を固定する考え方は,塗り分けのパターンを数える場合などに役立ちます。
どちらの考え方でも,この\(5\)人の円順列は\(4!\)通りあることが分かりました。 \(n\)個のものの円順列についても,次が成り立ちます。
異なる\(n\)個のものの円順列の総数は次の通りになる。
数珠順列
もうひとつ円形の並びを考えてみましょう。 今度は白・赤・緑・青・黒の\(5\)色の玉を\(1\)個ずつ使って,円形のブレスレットを作ります。 どれだけの種類のブレスレットを作れるでしょうか?
この問題も円順列と同じく\(4!\)で計算しようとすると,間違いです。 次の\(2\)つの並びは,円順列としては別物ですが,ブレスレットとしては全く同じものです。 ブレスレットは裏返すことができ,この\(2\)つの並びは裏返すことで一致するからです。
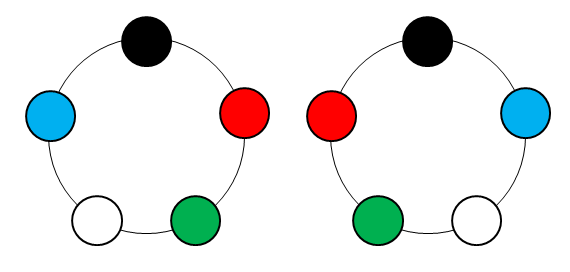
円順列を考えるときは,裏返して一致するものも別々に数えています。 ですからブレスレットの総数は,円順列の総数の半分になります。
このように裏返すこともできる円形の並びを数珠順列といいます。 数珠やネックレス,ブレスレットなどを考えるときの順列です。 数珠順列の総数は,先ほどの例で見た通り,円順列の総数の半分です。
異なる\(n\)個のものの数珠順列の総数は次の通りになる。
円形の並びを考えるとき,それが円順列か数珠順列かに気を付けましょう。 手に取って裏返すことができるようなら数珠順列です。
塗り分けの問題
円順列の応用例として,色の塗り分け問題を考えてみましょう。
次の図形は\(5\)つの四角形から成っています。 これを\(5\)色で塗り分ける方法は何通りあるでしょうか? 図形を回転して一致する塗り方は区別しません。

どう考えたら良いか,過去の経験から学びます。 例えば\(1\)列に並べる順列を考えるときは,左端から順にあり得るパターンを確定させていきました。 左端は\(5\)通り,その隣は\(4\)通り,…といった感じですね。
塗り分け問題を考えるときも同様に,少しずつ順番に色を確定していきます。 どんな順番で色を確定していくかで難易度が変わります。
この問題では,四角形は\(5\)つありますが,真ん中の四角形は周りの四角形とは性質が違いそうです。 真ん中の色から決めてしまいましょう。 真ん中の色は\(5\)色から選べるので,その選び方は\(5\)通りあります。
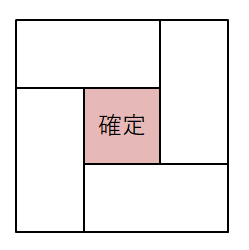
あとは周りの色を決めるのですが,これは円順列になりますね。 これらの塗り方は\((4 - 1)! = 3!\)通りです。
以上から,この図形の塗分け方の総数は次の数だけあります。
塗分け問題を考えるときは,どこから色を確定していくかが重要です。 他とは性質が違うところから色を塗っていきましょう。
確認問題
\(1\)と書かれたカードが\(1\)枚,\(2\)と書かれたカードが\(2\)枚,\(3\)と書かれたカードが\(3\)枚あります。 同じ番号のカードを区別しないとき,この\(6\)枚のカードを\(1\)列に並べる方法は何通りあるか答えてください。
答え
同じ番号のカードを区別する場合なら,\(6\)枚のカードを\(1\)列に並べる方法は\(6!\)通りです。 しかし,同じ番号のカードを区別しない場合,並べ方の総数はもっと少なくなります。
例えば,同じ番号のカードには別の色を付けて区別できるようにすると,次のカードの\(2\)つの並びは別物です。
しかし,同じ番号を区別しない場合は,この\(2\)つの並びは全く同じです。 \(6!\)で計算した場合の数は,このような並びを重複して数えているのです。
円順列の場合の数を求めるとき,重複して数えた分を調整しましたね。 ここでも重複分の調整をしていきます。
まず\(2\)のカードが\(2\)枚ありますから,そこに注目します。 カードを左から順に確認するとき,\(2\)のカードの登場順は,\(2!\)通りあります。 念のため確認しておくと,次の\(2\)つの場合ですね。
このそれぞれの場合について,\(3\)のカードの並びは\(3!\)通りあります。 つまり,\(2\)のカードと\(3\)のカードの並び方は,組み合わせると次の数だけあることが分かります。
\(2\)と\(3\)のカードの並びのパターンがこれだけあるということは,\(6!\)で計算した場合の数は,この数の分だけ重複して数えた結果だということです。 したがって,重複分を取り除くと,同じ番号を区別しない場合の並び方の総数は,次の計算で求められることが分かります。
というわけで,答えは\(60\)通りでした。
次の問いに答えてください。
-
\(5\)個のビーズを机の上で円形に並べる方法が何通りあるか答えてください。
-
\(5\)個のビーズに紐を通してブレスレットを作るとき,作れるブレスレットが何通りあるか答えてください。
答え
円順列と数珠順列を間違えないよう気を付けましょう。
-
机の上に並べるだけで,裏返すことはありませんから,これは円順列です。 異なる\(5\)個のものの円順列ですから,その総数は次の計算で求められ,\(24\)通りです。
\( \begin{align} (5 - 1)! = 4! = 24 \end{align} \) -
ブレスレットであれば裏返すことが可能であり,数珠順列の問題になります。 その総数は次の計算で求められ,\(12\)通りです。
\( \begin{align} \displaystyle\frac{(5 - 1)!}{2} = \displaystyle\frac{24}{2} = 12 \end{align} \)
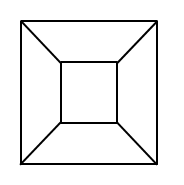
次の図形を\(5\)色で塗り分ける方法が何通りあるか答えてください。 ただし図形を回転して一致する塗り方は区別しません。
答え
どんな順番で塗る色を確定していくかが重要です。 まず真ん中の領域の色を決めることにすると,その色の選び方は\(5\)通りです。
このとき,残りの領域(周りの部分)の塗り分けは,残りの\(4\)色をどう円形に並べるかという円順列の問題になります。 したがって,この図形の塗り分け方の総数は,次の計算で求められます。
したがって,答えは\(30\)通りです。
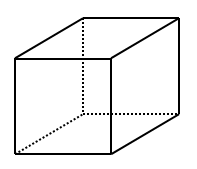
次の立方体の塗り分けについて,次の問いに答えてください。 ただし図形を回転して一致する塗り方は区別しません。
-
異なる\(6\)色を全て使って塗り分ける方法が何通りあるか答えてください。
-
異なる\(5\)色を全て使って塗り分ける方法が何通りあるか答えてください。
-
異なる\(4\)色を全て使って塗り分ける方法が何通りあるか答えてください。 異なる\(4\)つのものから\(2\)つを選ぶ方法が\(6\)通りであることを使って良いです。
-
異なる\(3\)色を全て使って塗り分ける方法が何通りあるか答えてください。
答え
どんな順番で塗る色を確定していくかが重要です。 特に特定の色が必ず使われる場合には,その色が塗られる面を固定してしまうと考えやすいです。 円順列の考え方と同じですね。
どの問題も全ての色を使うので,どの色も必ずどこかの面に塗られます。 立方体は回転できるので,ある特定の色を次図のように上側の面に来るようにできます。
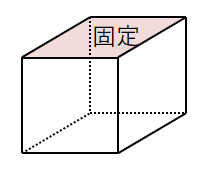
このように特定の色が特定の面に来るようにするルールを設ければ,ある色を上側の面に固定するという考え方ができます。
-
\(1\)つの色を塗る位置を上側の面に固定します。 残りの\(5\)色の塗り方を考えます。
まず塗った面の反対側の面を塗ります。 残りの\(5\)色から選んで塗るので,その塗り方は\(5\)通りです。
残りの\(4\)面はぐるっと一周しますから,その塗り方は円順列として考えられます。 数珠順列ではないことに注意してください。 上の面とその反対側の面は,異なる色で塗られていますから,例えば次のような\(2\)つの塗り方は別物になります。
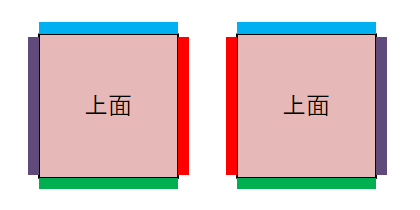
ちなみに,もし上の面とその反対側の面が同じ色であれば,この\(2\)つの塗り方は裏返せば一致しますから,数珠順列になります。
さて話を戻すと,ぐるっと一周する面の塗り方は\(4\)色の円順列ですから,立方体の塗り方は次の数だけあります。
\( \begin{align} 5 \times (4 - 1)! = 5 \times 6 = 30 \end{align} \)というわけで,答えは\(30\)通りです。
-
\(6\)色使う問題との違いは,色の種類が面の数より少ないことです。 このことで,\(2\)回使われる色が出てきます。 このことに注目しましょう。
使う色が\(5\)種類だけなので,\(1\)色だけ\(2\)回使わないといけません。 \(2\)回使う色は\(5\)色から選べるので,\(5\)通りあります。
塗り分けなので,隣り合う面が同じ色になってはいけませんから,同じ色は互いに反対側の面に塗るしかありません。 なので\(1\)組だけある同じ色を先に塗ってしまえば,後はぐるっと一周する\(4\)面を塗るだけです。
(1)でも解説した通り,この\(4\)面の塗り方は数珠順列になります。 上の面とその反対側の面が同じ色なので,次の\(2\)つのような塗り方が,立方体を裏返すことで完全一致するのです。

したがって,立方体の塗り方は次の数だけあります。
\( \begin{align} 5 \times \displaystyle\frac{(4 - 1)!}{2} = 5 \times \displaystyle\frac{6}{2} = 15 \end{align} \)というわけで,答えは\(15\)通りです。
-
色々な解き方ができます。 問題文の補足にある「組み合わせ」については,また後で学びます。
立方体に同じ色を塗るときは,互いに反対側の面に塗るしかありません。 そうでないと同じ色を塗った面が隣り合ってしまうからです。 したがって,使える色が\(4\)色しかない場合,\(2\)回使う色が\(2\)組あります。
逆に言えば,ある\(1\)組の向かい合う面だけが,異なる色で塗られることになります。 この向かい合う面の塗り方は,\(4\)色から\(2\)色を選ぶので,問題文の補足の通り\(6\)通りあります。
残りのぐるっと一周する\(4\)面の塗り方は,残りの\(2\)色を交互に塗るしかありませんから,その塗り方は\(1\)通りです。 以上から,立方体の塗り方は\(6\)通りです。
別の解き方も見てみましょう。 まずどの\(2\)色を\(2\)回使うか決めてしまいます。 その選び方は,問題文の補足の通り\(6\)通りです。
\(2\)回使う色の\(1\)組を互いに反対側の面に塗って固定します。 残りのぐるっと一周する\(4\)面の塗り方を考えます。 この\(4\)面にも同じ色を\(1\)組塗らなければなりません。 この\(4\)面も回転できますから,この\(1\)組を塗る位置を固定することができます。
残りの\(2\)面に残りの\(2\)色を塗るのですが,どちらの面にどちらの色を塗っても同じです。 どちらの塗り方も立方体を裏返せば一致するからです。
以上から,立方体の塗り方は\(6\)通りです。
-
先ほどの問題で見た通り,同じ色を\(3\)つの面に塗ることはできません。 したがって,\(3\)色とも\(2\)回ずつ使うしかなく,同じ色は互いに反対側に塗るしかありません。
とりあえずその内の\(1\)組を適当な面とその反対側に塗りましょう。 すると,残りのぐるっと一周する\(4\)面には,残りの\(2\)色を交互に塗るしかありません。
以上から,立方体を\(3\)色で塗り分ける場合,塗り方の自由度は一切なく,その総数は\(1\)通りしかありません。
