組み合わせの基本的な計算練習です。

1. 異なる\(4\)つのものから\(2\)つを選ぶ組み合わせの数ですから，次の計算で求められます。

   \( \begin{align} {}_4\mathrm{C}_2 &= \displaystyle\frac{4 \cdot 3}{2 \cdot 1} \\[5pt] &= 6 \end{align} \)

   というわけで，答えは\(6\)通りです。

2. \(3\)のカードを\(2\)枚選ぶ方法は\({}_3\mathrm{C}_2\)通り，\(4\)のカードを\(3\)枚選ぶ方法は\({}_4\mathrm{C}_3\)通りあります。 そのどちらも行うわけですから，その組み合わせは積の法則で考えられます。

   \( \begin{align} {}_3\mathrm{C}_2 \times {}_4\mathrm{C}_3 &= \displaystyle\frac{3 \cdot 2}{2 \cdot 1} \times \displaystyle\frac{4 \cdot 3 \cdot 2}{3 \cdot 2 \cdot 1} \\[5pt] &= 3 \times 4 \\[5pt] &= 12 \end{align} \)

   というわけで，答えは\(12\)通りです。

3. \(3\)のカード\(2\)枚と\(4\)のカード\(3\)枚の選び方自体は，(2)で求めたように\(12\)通りあります。 あとはこの\(5\)枚を\(1\)列に並べるだけですから，その方法は次の数だけあります。

   \( \begin{align} 12 \times 5! &= 12 \times 120 \\[5pt] &= 1440 \end{align} \)

   というわけで，答えは\(1440\)通りです。 それぞれのカードの選び方に対して，その並べ方が\(5!\)通りあるので，このような計算になります。

組の区別の有無について十分に注意してください。 組の区別をしないとき，重複して数えた分の調整が必要になります。

1. 計\(10\)枚からまず\(2\)枚を選ぶ方法は，\({}_{10}\mathrm{C}_2\)通りです。 次に残り\(8\)枚から\(3\)枚を選ぶ方法は，\({}_8\mathrm{C}_3\)通りです。 これで\(2\)枚と\(3\)枚の組ができ，残りの\(5\)枚も自動的に組になります。

   このように\(2\)枚，\(3\)枚を順に選ぶことで，組分けできるわけですから，組分けの総数は次の計算で求められます。

   \( \begin{align} {}_{10}\mathrm{C}_2 \times {}_8\mathrm{C}_3 &= \displaystyle\frac{10 \cdot 9}{2 \cdot 1} \times \displaystyle\frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} \\[5pt] &= 45 \times 56 \\[5pt] &= 2520 \end{align} \)

   というわけで，答えは\(2520\)通りです。

2. 先ほどと同様に考えると，組分けの方法を次の計算で求められそうです。

   \( \begin{align} {}_{10}\mathrm{C}_2 \times {}_8\mathrm{C}_4 &= \displaystyle\frac{10 \cdot 9}{2 \cdot 1} \times \displaystyle\frac{8 \cdot 7 \cdot 6 \cdot 5}{4 \cdot 3 \cdot 2 \cdot 1} \\[5pt] &= 45 \times 70 \\[5pt] &= 3150 \end{align} \)

   しかし，ひとつ問題があります。 「先に作った\(4\)枚組」と「後に作った\(4\)枚組」が区別されてしまっているのです。 この問題では単に組分けをするだけなので，\(2\)つの\(4\)枚組を区別しません。

   したがって，「先に作った\(4\)枚組」と「後に作った\(4\)枚組」の作った順番による区別をなくすため，\(2!\)で割って調整する必要があります。

   \( \begin{align} \displaystyle\frac{3150}{2!} = 1575 \end{align} \)

   というわけで，答えは\(1575\)通りです。

3. これまでと同様に考えます。 まず\(2\)枚組を\(4\)つ作ることを考えます。 最後の\(1\)組は残りの\(2\)枚のカードで自動的に決まります。

   \( \begin{align} &\quad {}_{10}\mathrm{C}_2 \times {}_8\mathrm{C}_2 \times {}_6\mathrm{C}_2 \times {}_4\mathrm{C}_2 \\[5pt] &= \displaystyle\frac{10 \cdot 9}{2 \cdot 1} \times \displaystyle\frac{8 \cdot 7}{2 \cdot 1} \times \displaystyle\frac{6 \cdot 5}{2 \cdot 1} \times \displaystyle\frac{4 \cdot 3}{2 \cdot 1} \\[5pt] &= 45 \times 28 \times 15 \times 6 \end{align} \)

   この数は\(5\)つの\(2\)枚組を区別したときの場合の数です。 この区別をなくす必要がありますから，\(5\)つの組を作る順番の数である\(5!\)で割る必要があります。

   \( \begin{align} \displaystyle\frac{45 \times 28 \times 15 \times 6}{5!} &= \displaystyle\frac{45 \times 28 \times 15 \times 6}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\[5pt] &= 945 \end{align} \)

   というわけで，答えは\(945\)通りです。 このように，分数の計算をするときは，途中で大きな数の計算をせずに，後で約分することをオススメします。

図形をかきながら考えるとイメージしやすいと思います。 また対角線や三角形を重複して数えないように，数え方に注意しましょう。

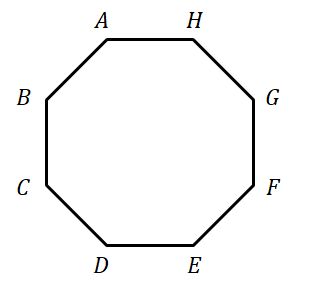
1. 対角線は，次図のように頂点を\(2\)つ選んで結ぶことでできます。

   

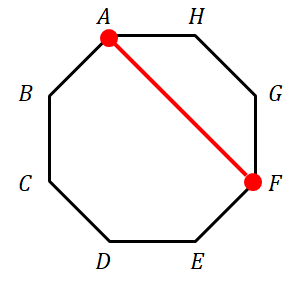
   しかし，次のように隣り合う\(2\)頂点を選んだ場合だけは，対角線にはなりません。 これは正八角形の辺ですね。

   

   したがって，対角線の本数は，\(8\)頂点から\(2\)つを選ぶ組み合わせの数から正八角形の辺の数を引けば求められます。

   \( \begin{align} {}_8\mathrm{C}_2 - 8 &= \displaystyle\frac{8 \cdot 7}{2 \cdot 1} - 8 \\[5pt] &= 28 - 8 \\[5pt] &= 20 \end{align} \)

   というわけで，答えは\(20\)本です。

2. 三角形は，頂点を\(3\)つ選んでそれぞれ結べばできます。 ですから，その個数は次の計算で求められます。

   \( \begin{align} {}_8\mathrm{C}_3 &= \displaystyle\frac{8 \cdot 7 \cdot 6}{3 \cdot 2 \cdot 1} \\[5pt] &= 56 \end{align} \)

   というわけで，答えは\(56\)個です。

3. 全ての三角形の個数は(2)で求めました。 この個数から「正八角形と辺を共有する三角形の個数」を引きましょう。

   そのような三角形には，辺を\(1\)つだけ共有するものと，辺を\(2\)つ共有するものがあります。 それぞれの三角形の個数を調べていきましょう。

   まず辺を\(1\)つだけ共有する三角形の個数を調べます。 共有する\(1\)辺の選び方は\(8\)通りあります。 そのそれぞれの場合について，三角形の残りの\(1\)頂点の選び方は，下図の×印のように\(4\)通りずつあります。

   

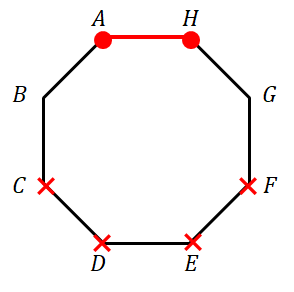
   これらの三角形は全て異なるものです。 共有する\(1\)辺か他の\(1\)頂点がそれぞれ異なるからです。 したがって，辺を\(1\)つだけ共有する三角形の個数は，次の計算で求められます。

   \( \begin{align} 8 \times 4 = 32 \end{align} \)

   次に辺を\(2\)つ共有する場合を考えます。 これは次図のような場合で，共有する\(2\)辺の選び方は\(8\)通りあります。 分かりづらければ，\(2\)辺の間の頂点に注目してください。 頂点の選び方は\(8\)通りしかありませんね。

   

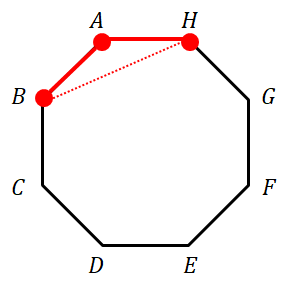
   残りの\(1\)辺も勝手に決まることが図から分かります。 したがって，\(2\)辺を共有する三角形は\(8\)個だけです。

   以上から，正八角形と辺を共有しない三角形は，次の計算の通り\(16\)個あります。

   \( \begin{align} 56 - 32 - 8 = 16 \end{align} \)

4. \(3\)辺の長さが異なるものといわれても考えづらいですね。 \(2\)辺または\(3\)辺の長さが等しい三角形の数を数えて，その数を(2)で求めた数から引きましょう。

   まず\(2\)辺のみが等しい三角形，つまり二等辺三角形を数えます。 頂角の選び方は\(8\)通りありますね。 このとき，\(2\)つの底角の選び方は，次図のように\(3\)通りあります。

   

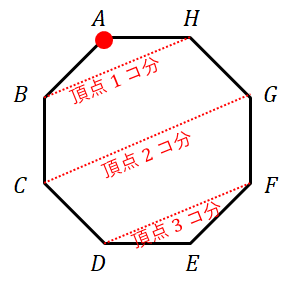
   二等辺三角形なので，頂角から左右に同じ数だけ移動した頂点が底角になります。 正八角形の場合は，先の図のように頂点\(1\)～\(3\)個分だけ移動した底角を考えられるわけですね。

   これで二等辺三角形の個数は\(8 \times 3\)個…とする前に，重複して数えたものがないかを確認する必要があります。 重複するのは，底角が他の二等辺三角形の頂角にもなる場合です。 このとき，三角形の全ての角度が等しくなるので，三角形は正三角形になりますね。

   しかし，どの二等辺三角形も正三角形にはなりません。 その確認のためには，先ほど見た\(3\)種類の二等辺三角形について，頂角の角度が\(60^{\circ}\)でないことを確認すれば良いです。 例えば次の二等辺三角形を見てください。

   

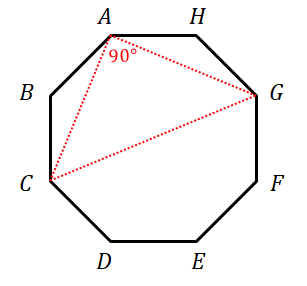
   正八角形の内角の大きさは次の通りですね。

   \( \begin{align} 180^{\circ} \times \displaystyle\frac{8 - 2}{8} = 135^{\circ} \end{align} \)

   \(\triangle \mathrm{ABC}\)が二等辺三角形であることを考慮すると，次のことが分かります。

   \( \begin{align} 2\angle \mathrm{BAC} &= 180^{\circ} - 135^{\circ} \\[5pt] &= 45^{\circ} \end{align} \)

   したがって，二等辺三角形\(\triangle \mathrm{ACG}\)の頂角の大きさが分かります。

   \( \begin{align} \angle \mathrm{CAG} &= 135^{\circ} - 2\angle \mathrm{BAC} \\[5pt] &= 135^{\circ} - 45^{\circ} \\[5pt] &= 90^{\circ} \end{align} \)

   これで\(\triangle \mathrm{ACG}\)が正三角形でないことがはっきりしました。 同様に\(\triangle \mathrm{ABH}\)，\(\triangle \mathrm{ADF}\)も正三角形でないことが確認できます。

   したがって，先ほどの\(8 \times 3\)で重複なく二等辺三角形を数えられていますから，二等辺三角形の個数は\(24\)です。 また，正三角形が存在しないことも分かりましたから，\(3\)辺の長さが互いに異なる三角形の個数は，次の計算の通り\(32\)個です。

   \( \begin{align} 56 - 24 = 32 \end{align} \)