前回学んだ組み合わせの計算には,様々な活用方法があります。 色々な応用問題を確認してみましょう。
目次
区別と順列
これまで学んだ順列や組み合わせの公式は,並べたり選んだりする対象が互いに異なる場合に適用できるものでした。 そこに同じものや区別しないものが含まれている場合,公式をそのまま適用することはできません。
公式を適用できなくなるのは,同じ並び順や選び方を何度か重複して数えてしまうからです。 どうして重複が発生するのかを理解し,どう対応すれば良いのかを学びましょう。
実は既に確認問題などで取り扱った話題ですが,ここで改めて整理しておきます。
例として,次のカードを\(1\)列に並べる方法を数えてみましょう。
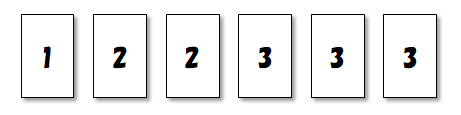
同じ番号でも区別できるとしたら,並べ方は\(6!\)通りですね。 問題は,同じ番号を区別できない場合です。 この場合,互いに異なるものの順列ではないので,公式を使って\(6!\)と計算することはできません。
ではどうすれば良いでしょう? 分かりやすいように,同じ番号のカードに下図のように異なる色を塗って考えます。
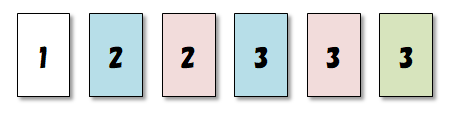
次の\(2\)つの並び順を見てください。 これらは,同じ番号のカードを区別できるなら,異なるものです。 しかし,カードに書かれた番号をよく見てください。 両者は全く同じものですね。
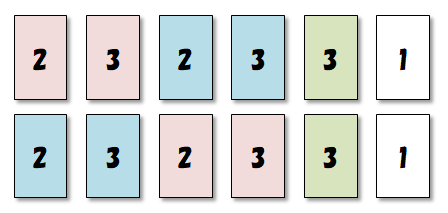
つまり,同じ番号が区別できない場合には,このような重複した並びを排除する必要があります。 そこで,\(1\)つの並びにつき,どれだけ重複した並びが存在するのかを確認しましょう。
まず\(2\)のカードに注目します。 \(2\)のカードは\(2\)枚ありますから,その並び順は,次図のように\(2!\)通りがあります。 そしてその並びのどれも,同じ番号を区別しない場合には同じものです。
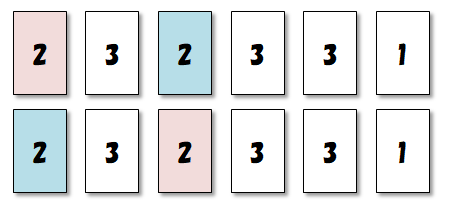
次に\(3\)のカードに注目します。 \(3\)のカードは\(3\)枚ありますから,その並び順は,次図のように\(3!\)通りがあります。 そしてその並びのどれも,同じ番号を区別しない場合には同じものです。
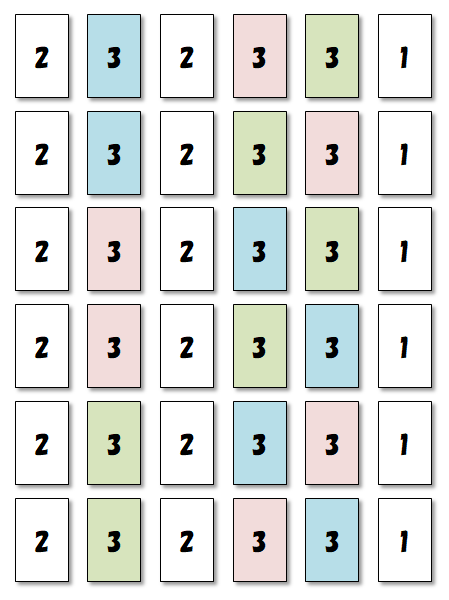
これらを組み合わせると,\(1\)つの並びにつき,\(2! \times 3!\)通りの重複した並びが存在することが分かります。 つまり,\(6!\)という数は,\(1\)つの並びをこれだけの回数重複して数えた結果なのです。
したがって,同じ番号を区別できない場合の並び順の総数は,次の計算によって求められます。
このように,区別できないものの並び順がいくつあるかを考えることで,公式を使った計算結果に潜む重複がどれだけあるか分かります。 その分の調整をしてあげれば良いわけですね。
区別と組分け
今までの確認問題でも何回か扱いましたが,組分けの問題について改めて考えます。 組の人数の指定などがない場合は,重複順列で考えましたね。
今回考えるのは,組の人数の指定や制限がある場合で,多くの場合は組み合わせの考え方を使います。 前回の確認問題でも扱いました。
組の区別の有無で組分けの総数が変わることは,これまで見てきました。 他にも組分けされるものの区別の有無でも,組分けの総数は変わります。 その点を整理すると,組分け問題には次の\(4\)パターンがあります。
| No. | 分けるものの区別 | 組の区別 |
|---|---|---|
| \(1\) | あり | あり |
| \(2\) | あり | なし |
| \(3\) | なし | あり |
| \(4\) | なし | なし |
男子\(3\)人,女子\(4\)人の計\(7\)人を\(2\)人,\(2\)人,\(3\)人の\(3\)組に分けることを例にして,それぞれのパターンで組分けの数を考えてみましょう。 ここで「分けるものの区別」は,男子同士の区別と女子同士の区別のこととします。
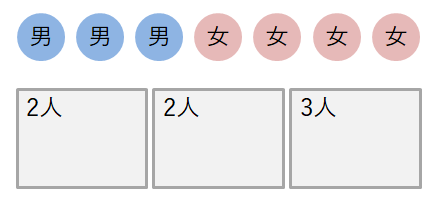
(1) まず人も組も区別する場合ですが,これはまず\(7\)人から\(2\)人を選んで\(2\)人組をつくり,次に残り\(5\)人から\(2\)人を選び\(2\)つめの\(2\)人組をつくれば良いです。 残された\(3\)人が残りのもう\(1\)組になります。
(2) 次に人は区別するが,組は区別しない場合です。 このとき(1)と違って,\(1\)つめの\(2\)人組と\(2\)つめの\(2\)人組の区別がなくなるので,これらの組をつくる順番の違いを排除します。
(3) 男子同士,女子同士は区別せず,組は区別する場合,問題になるのは各クラスの男女構成です。 男子も女子も十分な数いれば自由な組み合わせがありえますが,それぞれ\(3\)人と\(4\)人しかいないので,具体的にありえる組分けを書きだしてみましょう。
男女が十分な数いれば,各クラスに男女を好きな人数だけ入れられます。 例えば\(2\)人組の男女構成は,男子の人数が\(0\)人の場合,\(1\)人の場合,\(2\)人の場合の\(3\)通りがあります。 同様に考えれば,\(3\)人組の男女構成は\(4\)通りありますから,組分けパターンは次の数だけあります。
しかし今回の問題の場合,男女の人数は決まっており,例えば「どのクラスも女子だけ」といった組分けは存在しません。 したがって,このような単純な計算はできないのです。
\(1\)つめの\(2\)人組は「男男」か「男女」か「女女」のどれかになります。 まず\(1\)つめの\(2\)人組が「男男」の場合を考えます。
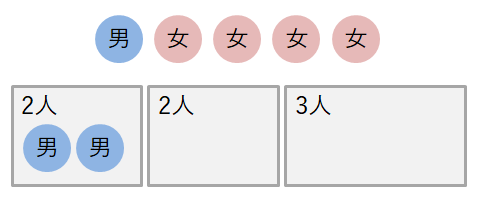
このとき,男子\(1\)人と女子\(4\)人が残っていますから,\(2\)つめの\(2\)人組は「男女」と「女女」の場合がありえます。 最後の\(3\)人組は残りの\(3\)人で自動的に決まりますから,この場合の組分けは次の\(2\)通りだけです。
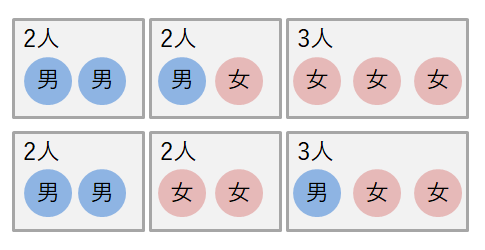
次に\(1\)つめの\(2\)人組が「男女」の場合を考えます。 この場合,\(2\)つめの\(2\)人組は「男男」,「男女」,「女女」のどれでもありえますから,この場合の組分けは\(3\)通りです。
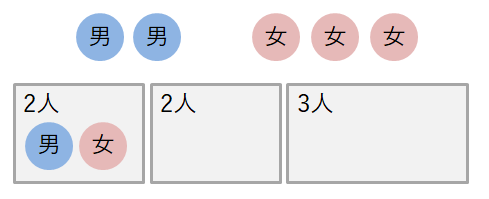
最後に\(1\)つめの\(2\)人組が「女女」の場合を考えます。 この場合,\(2\)つめの\(2\)人組は「男男」,「男女」,「女女」のどれでもありえますから,この場合の組分けは\(3\)通りです。
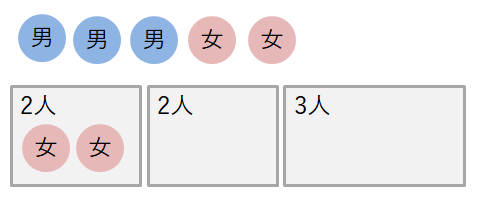
以上から,この問題の組分けの数は,次のようになります。
(4) 男子同士,女子同士を区別せず,組も区別しない場合,(3)から組の区別をなくせば良いです。
(3)では,次図の\(2\)通りの組分けのように,\(2\)つの\(2\)人組を入れ替えただけの組分けを重複して数えています。
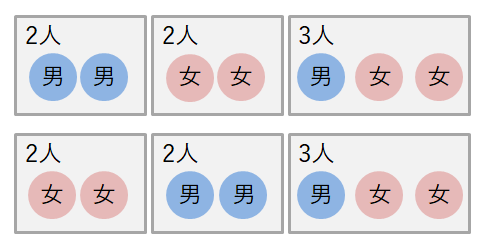
じゃあ,(3)の結果を\(2\)で割れば重複分を排除できる!というわけにはいきません。 \(2\)つの\(2\)人組が同一の男女構成の場合は,そもそも重複して数えていないからです。
男子が\(3\)人しかいないので,\(2\)人組が両方とも「男男」になることはありません。 しかし,両方とも「男女」か「女女」になる場合があります。
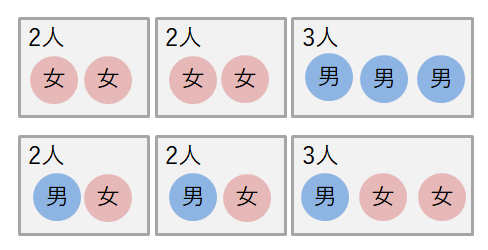
(3)の\(8\)通りのうち,この\(2\)通りだけは重複して数えられていないわけです。 したがって,(4)の組分けの数は,次の通りになります。
もちろん,この問題なら答えの場合の数はそんなに大きくないので,具体的にありえる組分けを書きだしてみても良いです。 しかし,答えが大きくなる問題にも対応するためには,このような考え方に慣れる必要があります。
最短経路
最後に定番問題である最短経路を考えます。 次の図は,ある世界の格子状の道を表しています。 平安京とかの道だと思ってください。 スタート\(\mathrm{S}\)からゴール\(\mathrm{G}\)までの最短経路は何種類あるでしょうか?
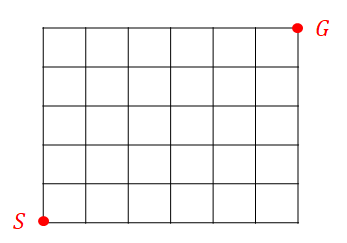
どんな道順が最短になるかは,難しい話ではありません。 寄り道さえしなければ最短なので,例えば次のような道順も最短経路です。
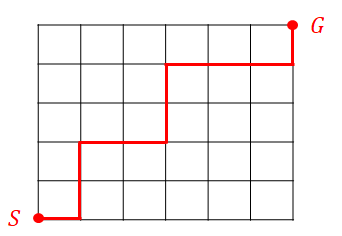
このような最短経路の本数を数えるために,問題を単純化しましょう。 スタートからゴールまで,右に\(6\),上に\(5\)だけ移動すれば良いのですから,この問題は「\(6\)つの\(\rightarrow\)と\(5\)つの\(\uparrow\)の並べ方は何通りあるか?」という問題に言い換えられます。
例えば先ほどの道順の例は,次の矢印の並びと対応します。
同じ矢印を区別する必要はありませんから,この問題は前々項で学んだ類のものです。 矢印の並び順の総数は,次の計算で求められますね。
この数が,先ほどの図における最短経路の数になります。 確認問題でもう少し幅広い問題にも挑戦してみましょう。
確認問題
次の文字列を並び替えて新しい文字列をつくるとき,(1)~(3)に答えてください。
-
できる文字列が何種類あるか答えてください。
-
全ての\(\mathrm{s}\)が連続して並ぶ文字列が何種類あるか答えてください。
-
\(\mathrm{a}\)と\(\mathrm{c}\)がこの順に並ぶ文字列が何種類あるか答えてください。
答え
同じ文字がいくつか含まれていますから,そこに注意して解いていきましょう。 並び替える文字列に含まれる文字とその個数は,次の通りです。
| 文字 | 個数 |
|---|---|
| \(\mathrm{s}\) | \(3\) |
| \(\mathrm{t}\) | \(3\) |
| \(\mathrm{i}\) | \(2\) |
| \(\mathrm{a}\) | \(1\) |
| \(\mathrm{c}\) | \(1\) |
-
同じ文字がいくつかあることによって,\(10!\)で文字列の数を計算することはできません。 これは同じ文字の並び順の組み合わせ分だけ重複して数えた結果なので,その分を調整しましょう。
\( \begin{align} &\quad \displaystyle\frac{10!}{3! \times 3! \times 2!} \\[5pt] &= \displaystyle\frac{10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3 \cdot 2 \cdot 1 \cdot 3 \cdot 2 \cdot 1 \cdot 2 \cdot 1} \\[5pt] &= 50400 \end{align} \)これでできる文字列が\(50400\)種類あることが分かりました。
-
\(3\)つの\(\mathrm{s}\)が\(\mathrm{sss}\)という塊になると考えましょう。 このとき,文字列を構成するものは次の通りになります。
文字 個数 \(\mathrm{sss}\) \(1\) \(\mathrm{t}\) \(3\) \(\mathrm{i}\) \(2\) \(\mathrm{a}\) \(1\) \(\mathrm{c}\) \(1\) したがって,これら\(8\)つの構成要素からなる文字列を考えれば良いので,その数は次のように計算できます。
\( \begin{align} &\quad \displaystyle\frac{8!}{3! \times 2!} \\[5pt] &= \displaystyle\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3 \cdot 2 \cdot 1 \cdot 2 \cdot 1} \\[5pt] &= 3360 \end{align} \)これで条件を満たす文字列が\(3360\)種類あることが分かりました。
-
\(2\)つの解き方を紹介します。 まずは文字列の枠が下のように\(10\)個あると考えます。
\( \begin{align} \Box\Box\Box\Box\Box\Box\Box\Box\Box\Box \end{align} \)そしてこの内\(2\)つの枠には\(\mathrm{a}\),\(\mathrm{c}\)がこの順に入ります。 \(\mathrm{a}\),\(\mathrm{c}\)を入れる\(2\)つの枠の選び方の総数は,次の通りです。
\( \begin{align} {}_{10} \mathrm{C}_2 \end{align} \)これで確保した\(2\)つの枠に,左から順に\(\mathrm{a}\),\(\mathrm{c}\)を入れれば良いですね。 あとは残りの\(8\)文字を他の\(8\)枠に並べるだけですから,結局できる文字列の総数は次の通りです。
\( \begin{align} &\quad {}_{10} \mathrm{C}_2 \times \displaystyle\frac{8!}{3! \times 3! \times 2!} \\[5pt] &= \displaystyle\frac{10 \cdot 9}{2 \cdot 1} \times \displaystyle\frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3 \cdot 2 \cdot 1 \cdot 3 \cdot 2 \cdot 1 \cdot 2 \cdot 1} \\[5pt] &= 25200 \end{align} \)これで条件を満たす文字列が\(25200\)種類あることが分かりました。
もうひとつの解き方は,\(\mathrm{a}\),\(\mathrm{c}\)を入れる枠を\(\Box\)と表しておいて,次の構成要素の並びを考えるものです。
文字 個数 \(\mathrm{s}\) \(3\) \(\mathrm{t}\) \(3\) \(\mathrm{i}\) \(2\) \(\Box\) \(2\) これらを並べてできた文字列には\(2\)つの\(\Box\)があります。 これら\(\Box\)に左から順に\(\mathrm{a}\),\(\mathrm{c}\)を入れれば良いので,この\(\Box\)を含めた文字列の個数を数えれば良いです。
\( \begin{align} &\quad \displaystyle\frac{10!}{3! \times 3! \times 2! \times 2!} \\[5pt] &= 25200 \end{align} \)これで同じく条件を満たす文字列が\(25200\)種類あることが分かりました。
次の問いに答えてください。
-
赤玉\(3\),青玉\(4\)個,緑玉\(1\)個があります。 同じ色の玉を区別しないとき,これらを円形に並べる方法が何通りあるか答えてください。
-
(1)で円形に並べた玉に紐を通してネックレスを作ります。 何通りのネックレスができるか答えてください。
答え
円順列・数珠順列の問題ですが,区別できないものが含まれています。 異なるものの円順列・数珠順列ではないので,今までに学んだ公式をそのまま適用することはできません。
-
円順列を考えるときは,並べるものの\(1\)つを固定すると考えやすいです。 \(1\)個しかない緑玉の位置を固定しましょう。
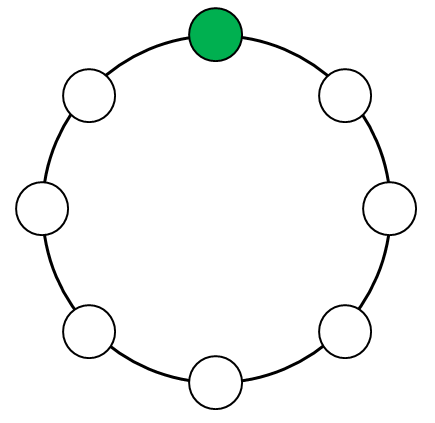
そうすると,あとは赤玉\(3\)個,青玉\(4\)個の並べ方を考えるだけで済みます。
\( \begin{align} &\quad \displaystyle\frac{7!}{3! \times 4!} \\[5pt] &= \displaystyle\frac{7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{3 \cdot 2 \cdot 1 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\[5pt] &= 35 \end{align} \)これで題意の並べ方が\(35\)通りあることが分かりました。
-
円順列から数珠順列を考えるとき,\(2\)で割っていましたね。 あれは,どの円順列も裏返せば別の円順列になったので,\(2\)で割ることで重複なしの個数を数えられたのです。
しかし,この問題のように同じものを含む円順列は,裏返しても別の円順列にならない,つまり左右対称のものが含まれています。 左右対称の円順列については,\(2\)回重複して数えられていないので,\(2\)で割ってはいけません。
というわけで,まず左右対称の円順列がいくつあるかを確認し,それ以外の個数を\(2\)で割ることで数珠順列の数が分かります。 左右対称のものを考えると,緑玉と赤玉は奇数個なので,それぞれ\(1\)つは対称軸上に置く必要があります。 下図で緑玉と赤玉を結ぶ直線を対称軸として考えましょう。
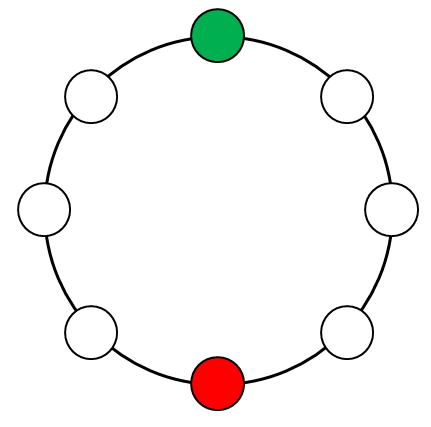
残り\(2\)個の赤玉を左右対称に置く必要があるので,その配置は次の\(3\)通りしかありません。
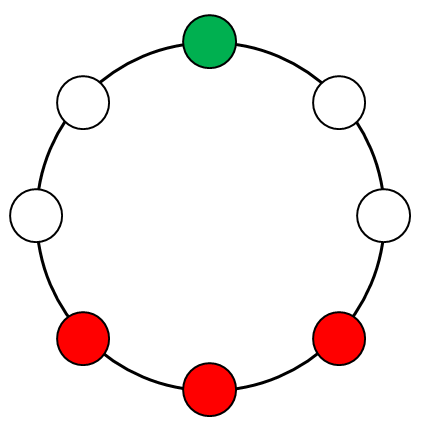
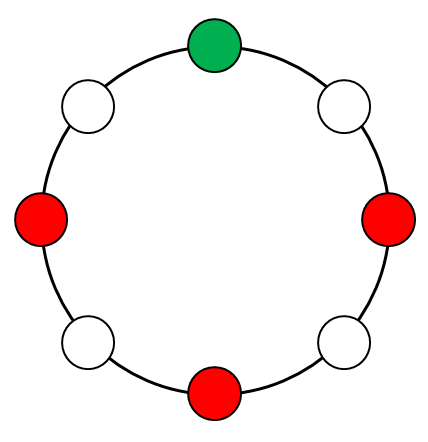
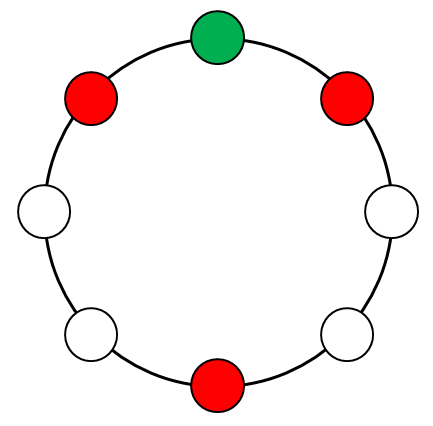
残りの玉は青玉なわけですね。 というわけで,左右対称の円順列は\(3\)通りあったので,左右非対称の円順列は(1)より\(32\)通りだけであることが分かります。 左右非対称の円順列は,数珠順列としては\(2\)回ずつ数えられることになるので,この数珠順列の数は次の通りです。
\( \begin{align} 3 + \displaystyle\frac{32}{2} = 19 \end{align} \)これでネックレスが\(19\)通りあることが分かりました。
玉が\(3\)個まで入る箱が\(3\)つあります。 これらに\(5\)個の玉を分けていれます。 玉を入れない箱があっても構いません。
次の各場合について,玉の分け方が何通りあるか答えてください。
-
玉も箱も区別する
-
玉は区別するが,箱は区別しない
-
玉は区別しないが,箱は区別する
-
玉も箱も区別しない
答え
区別の有無によっては,場合の数を単純な計算で求められないこともあります。 場合の数の計算の意味を理解し,計算できないものは具体的に書きだすなど,柔軟に対応しましょう。
-
箱に入る玉の数に制限がなければ,それぞれの玉に対して入れる箱が\(3\)通りずつあるので,\(3^5\)で計算できました。 しかし,この問題ではそうはいきません。
この数は,ある箱に玉を\(4\)個以上入れてしまった場合を含んでいます。 ですから,ある箱に玉が\(4\)個入っている場合と\(5\)個入っている場合の数を引けばOKです。
ある箱に玉が\(4\)個入っている場合は,まず玉を\(4\)個入れる箱の選び方が\(3\)通りあり,その\(4\)個の玉の選び方が\({}_5 \mathrm{C}_4\)通りあります。 残り\(1\)個の玉を入れる箱の選び方が\(2\)通りあるので,ある箱に玉が\(4\)個入る場合の数は次の通りです。
\( \begin{align} 3 \times {}_5 \mathrm{C}_4 \times 2 \end{align} \)次にある箱に玉が\(5\)個,つまり全部入る場合の数は,どの箱に玉を全て入れるかを考えると\(3\)通りであることが分かります。
したがって,玉も箱も区別する場合の玉の分け方の総数は,次の通りです。
\( \begin{align} &\quad 3^5 - 3 \times {}_5 \mathrm{C}_4 \times 2 - 3 \\[5pt] &= 243 - 30 - 3 \\[5pt] &= 210 \end{align} \)というわけで,答えは\(210\)通りでした。
-
(1)の結果を利用する場合,箱の区別をなくせば良いです。 箱の区別を箱の並び順として考えれば,\(3\)つの箱の並び順の数で割れば良いことが分かります。
\( \begin{align} \displaystyle\frac{210}{3!} = 35 \end{align} \)というわけで,答えは\(35\)通りでした。
(1)を考慮せずに解くなら,まず玉の分け方にどんなパターンがあるかを考えます。 \(3\)つの箱の玉の数を\((x, y, z)\)のように表すと,ありえるのは次の\(3\)パターンです。
\( \begin{align} &(3, 2, 0) \\[5pt] &(3, 1, 1) \\[5pt] &(2, 2, 1) \end{align} \)それぞれのパターンの玉の選び方を考えましょう。 まず\((3, 2, 0)\)の場合ですが,\(3\)個入りの箱に入れる玉の選び方が\({}_5 \mathrm{C}_3\)通りで,この箱の玉の入れ方さえ決めてしまえば,残りの\(2\)箱への玉の入り方は自動的に決まります。
したがって,このパターンの玉の分け方の数は,次の通りです。
\( \begin{align} {}_5 \mathrm{C}_3 = 10 \end{align} \)\((3, 1, 1)\)の場合も同様に,\(3\)個入りの玉の選び方さえ決まれば,残り\(2\)箱の玉の入れ方が自動的に決まります。
したがって,このパターンの玉の分け方の数は,次の通りです。
\( \begin{align} {}_5 \mathrm{C}_3 = 10 \end{align} \)\((2, 2, 1)\)の場合は,まず\(1\)個入りの箱に入れる玉の選び方が\(5\)通りですね。 残りの\(4\)個の玉を\(2\)個ずつに分ける方法は,ある\(1\)つの玉に注目すると分かりやすいです。 この玉を\(\mathrm{A}\)とすると,どちらかの箱には必ず\(\mathrm{A}\)が入っているわけですから,これとペアになる玉の選び方を数えれば良いです。 その選び方は,\(\mathrm{A}\)以外に残った\(3\)個から選ぶのですから,\(3\)通りです。
したがって,このパターンの玉の分け方の数は,次の通りです。
\( \begin{align} 5 \times 3 = 15 \end{align} \)以上を合わせると,題意の玉の分け方の数は,次の通りだと分かります。
\( \begin{align} 10 + 10 + 15 = 35 \end{align} \)というわけで,答えは\(35\)通りでした。
-
玉に区別がないのですから,重要なのはどの箱に何個の玉が入るかだけです。 箱の区別がない場合,箱に入れる玉の数の組み合わせは,(2)の別解でも見た通り,次の\(3\)パターンです。
\( \begin{align} &(3, 2, 0) \\[5pt] &(3, 1, 1) \\[5pt] &(2, 2, 1) \end{align} \)それぞれの組み合わせについて,箱を並び順で区別することで,箱の並べ方の総数を数えれば良いことが分かります。 \((3, 2, 0)\)の場合の並べ方は\(3!\)通りですね。
\((3, 1, 1)\)と\((2, 1, 1)\)の場合については,\(2\)つの箱の玉の数が同じです。 ですからその並べ方は,残り\(1\)つの箱を何番目に置くかで決まりますから,それぞれ\(3\)通りです。
したがって,題意の玉の分け方の総数は,次の通りです。
\( \begin{align} 3! + 3 + 3 = 12 \end{align} \)というわけで,答えは\(12\)通りでした。
-
最後が一番簡単な問題ですね。 箱の区別すらなくなったので,\(5\)個の玉を\(3\)つに分ける方法だけが問題です。 (2)でも(3)でも触れた通り,その分け方は次の\(3\)通りです。 これが答えです。
\( \begin{align} &(3, 2, 0) \\[5pt] &(3, 1, 1) \\[5pt] &(2, 2, 1) \end{align} \)
次の図は,ある世界の格子状の道を表しています。
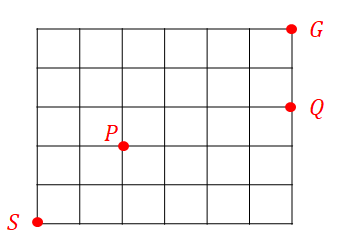
次の問いに答えてください。
-
\(\mathrm{S}\)から\(\mathrm{G}\)に至る最短経路が何本あるか答えてください。
-
\(\mathrm{S}\)から\(\mathrm{P}\)と\(\mathrm{Q}\)を経て\(\mathrm{G}\)に至る最短経路が何本あるか答えてください。
答え
本文中でも解説した通り,道順を矢印の並びとして表現すると良いです。
-
\(\mathrm{S}\)から\(\mathrm{G}\)へ最短でたどり着くには,右へ\(6\)回,上に\(5\)回移動すれば良いです。 右への移動を\(\rightarrow\),上への移動を\(\uparrow\)で表して,その並び順がいくつあるかを考えましょう。
同じ矢印がいくつか含まれていることを考慮すると,その並び順の総数は次の通りです。
\( \begin{align} &\quad \displaystyle\frac{11!}{6! \times 5!} \\[5pt] &= \displaystyle\frac{11 \cdot 10 \cdot 9 \cdot 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} \\[5pt] &= 462 \end{align} \)というわけで,答えは\(462\)本でした。
-
\(\mathrm{S}\)から\(\mathrm{P}\)へ最短でたどり着き,\(\mathrm{P}\)から\(\mathrm{Q}\)へ最短でたどり着き,\(\mathrm{Q}\)から\(\mathrm{G}\)へ最短でたどり着くという\(3\)段階で考えましょう。
\(1\)段階目では,右に\(2\)回,上に\(2\)回移動すれば良いので,その経路の数は次の通りです。
\( \begin{align} &\quad \displaystyle\frac{4!}{2! \times 2!} \\[5pt] &= \displaystyle\frac{4 \cdot 3 \cdot 2 \cdot 1}{2 \cdot 1 \cdot 2 \cdot 1} \\[5pt] &= 6 \end{align} \)\(2\)段階目では,右に\(4\)回,上に\(1\)回移動すれば良いので,その経路の数は次の通りです。
\( \begin{align} &\quad \displaystyle\frac{5!}{4!} \\[5pt] &= 5 \end{align} \)\(3\)段階目では,移動経路が\(1\)通りしかありませんね。
各段階の経路のとり方を組み合わせると,題意の移動経路の数は次の通りです。
\( \begin{align} 6 \times 5 \times 1 = 30 \end{align} \)というわけで,答えは\(30\)本でした。
次の図は,ある世界の格子状の道を表しています。

\(\mathrm{S}\)から\(\mathrm{G}\)に至る最短経路が何本あるか答えてください。
答え
下から行くルートや上から行くルートがあり,計算で求めるには色々場合分けが必要です。 それは面倒なので,何か別の手を考えます。
有名な方法として,図の各交差点に,そこに至る最短経路の本数を書いていくというものがあります。 次の図を見てください。 ある道の一部分の図です。
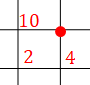
この図では,赤い点の周りの交差点について,その交差点に至る最短経路の本数が記されています。 このとき,赤い点に至る最短経路の本数はいくつでしょうか? (スタートは左下の方,ゴールは右上の方にあるとします。)
答えは\(14\)本です。 最短で移動するので,上側や右側の交差点から逆戻りすることはありません。 必ず下か左からこの点にやって来るので,それぞれの最短経路の数を合わせて\(14\)本なのです。
同様の考え方をこの問題にも適用してみましょう。 まず,\(\mathrm{S}\)からまっすぐ移動して到達できる交差点に至る最短経路は\(1\)本しかありません。
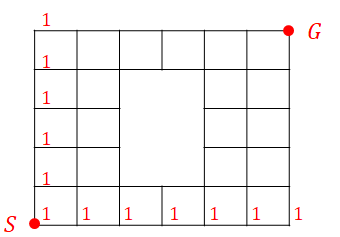
あとはこの図から,他の交差点へ至る最短経路の本数を書き込んでいくだけです。 下と左の交差点の数が分かっている交差点に,それらの数の和を書き込んでいけば良いですね。

というわけで,答えが\(162\)本であることが分かりました。 道が途切れていたり,変則的な形である場合には,場合分けで計算するよりもこの方法が有効です。
