重複組み合わせ

はじめに

場合の数の最後に，同じものを何度も取り出せる「重複組み合わせ」を考えます。柔軟に発想を転換することが必要です。

重複組み合わせ

▼

今まで考えてきた組み合わせは，同じものを何度も取り出したりできませんでした。しかしそれでは，次のような問題を考えるときに不都合です。

林檎と蜜柑と梨を合計\(10\)個買うことになりました。それぞれの個数の組み合わせは何通りあるでしょうか？ \(1\)個も買わない果物があっても構いません。

この問題を解くこと自体は難しくありません。次の補足のようにちょっとした場合分けで解けます。

補足解法例

まず林檎の個数の選び方は\(0\)個～\(10\)個の\(11\)通りあります。

例えば林檎を\(4\)個選ぶとき，蜜柑の選び方は\(0\)個～\(6\)個の\(7\)通りです。そして林檎と蜜柑の個数が決まれば，梨の個数も勝手に決まります。

同様に，林檎を\(n\)個選んだときの蜜柑・梨の選び方は\(11 - n\)通りです。したがって，林檎・蜜柑・梨の選び方の総数は，次の通りです。

\( \begin{align} 1 + 2 + 3 + \cdots + 10 + 11 = 66 \end{align} \)

しかし，せっかく「組み合わせ」に関する問題なのですから，今まで学んだ組み合わせの考え方を利用したいです。問題がもう少し複雑だと，補足の方法では手に負えないこともありますし。

組み合わせの考え方を使うために，少し工夫して考えます。次図のように，まず林檎・蜜柑・梨を置くための枠を\(10\)個用意します。

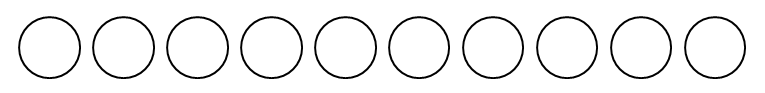
ここに選んだ林檎・蜜柑・梨を置くことにしましょう。並べる順番は問題と関係ないので，林檎を左の方に詰めて，その次に蜜柑，その次に梨を並べることにします。

そうすると，問題なのはどこを境に林檎と蜜柑，蜜柑と梨が切り替わるかです。その境目に下図のように仕切りを置くことにしましょう。仕切りで隔てられた\(3\)つの領域にそれぞれ林檎・蜜柑・梨を置くのです。

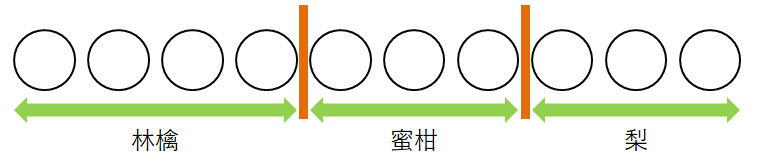
上図は林檎\(4\)個，蜜柑\(3\)個，梨\(3\)の場合です。もうひとつ例を見ておくと，次図は林檎\(0\)個，蜜柑\(3\)個，梨\(7\)個の場合を表します。

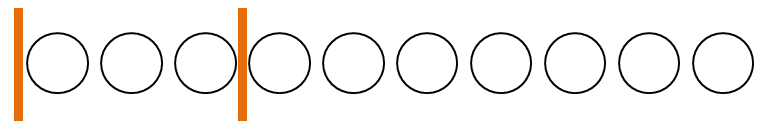
この\(10\)個の枠と\(2\)つの仕切りの並びこそが，林檎・蜜柑・梨の選び方を表します。なのでこれらの並べ方が何通りあるかを数えれば良いことになります。

枠同士や仕切り同士を区別する必要はありませんから，その並べ方の総数は次の通りです。

\( \begin{align} \displaystyle\frac{12!}{10!2!} = 66 \end{align} \)

この問題は，林檎・蜜柑・梨から重複を許して\(10\)個を選ぶ組み合わせを考えるものです。このような組み合わせを重複組み合わせといいます。

重複組み合わせを考えるときには，このような仕切りでグループ分けする方法を使います。確認問題も解きながら，この発想に慣れておきましょう。

補足重複組み合わせの公式

異なる\(n\)個のものから重複を許して\(r\)個を取り出して\(1\)組にするとき，その組み合わせの総数は次の計算で求められます。

\( \begin{align} \displaystyle\frac{(n + r - 1)!}{r!(n - 1)!} = {}_{n + r - 1}\mathrm{C}_r \end{align} \)

これを\({}_n\mathrm{H}_r\)と書きます。・・・が，わざわざ公式として覚えることはオススメしません。仕切りでグループ分けする発想を身につけるのが基本です。

ちなみに\(\mathrm{H}\)は同次積を英語で表した Homogeneous product から来ています。同次式（各項の次数が等しい式）の累乗（同次積）を計算したときに出てくる項について考えるとき，この重複組み合わせが役立つのです。その一例を確認問題で扱います。

確認問題

▲

\((x + y + z)^5\)を展開して出てくる項がいくつあるか答えてください。もちろん同類項はまとめます。

答え

\((x + y + z)^5\)を展開すると，\(5\)つの\(x + y + z\)から項を\(1\)つずつ選んで，それらの積をとってできた項が現れます。つまり，この式を展開して出てくる項というのは，\(x\)，\(y\)，\(z\)を合計\(5\)個組み合わせてできるものなのです。

これは，「異なる\(3\)つのものから重複を許して\(5\)個を選ぶ方法は何通りか？」という問題です。重複組み合わせの問題ですね。

本文のように図示してみます。 \(5\)個選ぶということで，まず\(5\)個の枠を用意しておき，それらをグループ分けするための仕切りを用意するわけです。選ぶものが\(x\)，\(y\)，\(z\)の\(3\)種類ありますから，仕切りは\(2\)つ必要ですね。

\(2\)つの仕切りによって，枠が\(3\)つの領域に分けられ，それぞれが\(x\)，\(y\)，\(z\)を置く領域になるわけですね。あとはこれらの枠と仕切りの並べ方を数えれば，それがそのまま\(x\)，\(y\)，\(z\)の選び方の個数，すなわち展開後の項の個数になるわけです。

\( \begin{align} \displaystyle\frac{7!}{5! \times 2!} = 21 \end{align} \)

というわけで，\((x + y + z)^5\)を展開して出てくる項は\(21\)個でした。

\(5\)個の区別しない玉を箱\(\mathrm{A}\)，箱\(\mathrm{B}\)，箱\(\mathrm{C}\)に分けて入れることを考えましょう。空っぽの箱があっても良いとするとき，玉の分け方は何通りあるでしょうか？

答え

玉を区別する場合は簡単です。それぞれの玉に対して，それを入れる箱は\(3\)通り選べるわけですから，玉の分け方は\(3^5\)通りです。

しかし，この問題では玉を区別しません。それぞれの箱に入る玉の個数はいくつか，この点だけが重要です。それを具体的に書きだすことは容易いですが，応用力を高めるためにも計算で求めましょう。

発想を逆転させると，これまで学んだことを応用できます。「それぞれの箱に玉がいくつ入るか？」という問題は，「それぞれの箱が何回選ばれるか？」という問題に言い換えられるのです。こう考えれば，重複組み合わせの問題になりますね。

例の如く枠と仕切りで図示します。玉の個数だけ箱を選ぶので，\(5\)個の枠と\(2\)個の仕切りを使います。仕切りで分けられた領域が，それぞれ箱\(\mathrm{A}\)，箱\(\mathrm{B}\)，箱\(\mathrm{C}\)の領域ですね。

この図を「\(5\)個の玉を\(2\)つの仕切りでグループ分けしたもの」と考えても良いです。玉自体に区別がないので，どの玉がどの箱に入るかを気にする必要がありませんよね。だから玉を単に\(3\)つのグループに分けて，それぞれ箱\(\mathrm{A}\)，箱\(\mathrm{B}\)，箱\(\mathrm{C}\)の領域とすればＯＫなのです。こう考えれば，別に重複組み合わせの問題でもないですね。

どう考えるにしても，玉の分け方の総数は，\(5\)つの枠（玉）と\(2\)つの仕切りの並び順の総数と等しいです。したがって，その数は次のように求められます。

\( \begin{align} \displaystyle\frac{7!}{5! \times 2!} = 21 \end{align} \)

というわけで，玉の分け方は\(21\)通りあります。

林檎と蜜柑と梨を合わせて\(10\)個買います。ただし，どの果物も最低\(1\)個は買わなければなりません。それぞれの個数の組み合わせが何通りあるか答えて下さい。

答え

本文でもうやった問題かと思いきや，少し違いがあります。どの果物も最低\(1\)個は買わなければならないという点ですね。枠と仕切りの図を見返してみます。

買わない果物があっても良いときは，ただこれらの枠と仕切りの並べ方を数えれば良かったです。しかしどの果物も買わないといけないので，仕切りで区切られたどの領域にも，枠が\(1\)つは必要です。

しかしそのような並べ方を考えるのは，非常に面倒です。そこで次のように考えてみましょう。各果物をあらかじめ\(1\)個ずつ確保しておくと。

こう考えれば，残り\(7\)個を買うだけです。しかも買わない果物があっても構いません。既にそれぞれ\(1\)個は確保しているのですから。あとは次の枠と仕切りの並びを考えるだけです。

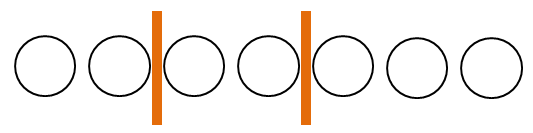
これらの枠・仕切りの並べ方の総数は，次の通りです。

\( \begin{align} \displaystyle\frac{9!}{7! \times 2!} = 36 \end{align} \)

というわけで，果物を買う個数の組み合わせは\(36\)通りあります。