前回,確率とは何かということを学びました。 今回は順列や組み合わせの計算を駆使して,確率の計算練習をします。
目次
確率の問題例
ここでは試しに\(1\)問だけ考えてみて,あとは確認問題としておきます。 次の問題を考えます。
\(5\)人でじゃんけんをして,あいこになる確率を求めてください。
明記はしていませんが,\(5\)人は超能力を持っていたりはしないので,どの手を出す事象も同様に確からしいと考えます。
まず全事象を考えると,それぞれの人の手の出し方は\(3\)通りありますから,\(5\)人の手の出し方の組み合わせは,次の数だけあります。
この内,あいこになる手の出し方が何通りあるかを数えます。 あいこになるのは,次のどちらかの場合です。
- 全員が同じ手を出す
- \(3\)種類の手が全て出る
まず全員が同じ手を出す場合を考えると,これは全員がグー,全員がチョキ,全員がパーのどれかしかありませんから,\(3\)通りだけです。
次に\(3\)種類の手が全て出る場合を考えます。 人は\(5\)人いますから,何人かは同じ手を出します。 同じ手の出し方には,同じ手を出す人が\(3\)人いる場合(次の\(1\)行目パターン)と,\(2\)種類の手を\(2\)人ずつが出す場合(次の\(2\)行目パターン)があります。
同じ手を出す人が\(3\)人いる場合,その同じ手の選び方は\(3\)通りあります。 残りの\(2\)人は,残りの\(2\)つの手を出すことになります。
どの手を誰が出すかは,この\(5\)つの手の並べ方を数えれば分かります。 並べた順に\(5\)人に手を割り当てれば良いのです。 したがって,この場合の手の出し方は次の数だけあります。
次に\(2\)種類の手を\(2\)人ずつが出す場合を考えます。 この\(2\)種類の手の選び方は\({}_3\mathrm{C}_2\)通りあり,残りの\(1\)人は残り\(1\)つの手を出すことになります。
どの手を誰が出すかは,この\(5\)つの手の並べ方を数えれば分かります。 したがって,この場合の手の出し方は次の数だけあります。
以上より,あいこになる手の出方の数は,次の通りです。
これで確率を次のように求められます。
このように確率の問題は,結局のところ場合の数さえ分かれば求められます。 今まで学んだ場合の数の知識を活かす場面です。 確認問題にも挑戦してみましょう。
確認問題
次の文字列をランダムに並び替えます。
同じ文字が連続して並ぶような文字列ができる確率を求めてください。
答え
まず文字列が全部で何通りできるか考えます。 文字列に使用される各文字の個数は次の通りです。
| 文字 | 個数 |
|---|---|
| \(\mathrm{s}\) | \(4\) |
| \(\mathrm{c}\) | \(2\) |
| \(\mathrm{e}\) | \(2\) |
| \(\mathrm{u}\) | \(1\) |
したがって,できる文字列の個数は次の通りです。
次に同じ文字が連続して並ぶような文字列が何通りあるか考えます。 同じ文字は一塊として扱うと考えやすいですね。 つまり,文字列の構成要素が次のようになっていると考えます。
| 文字 | 個数 |
|---|---|
| \(\mathrm{ssss}\) | \(1\) |
| \(\mathrm{cc}\) | \(1\) |
| \(\mathrm{ee}\) | \(1\) |
| \(\mathrm{u}\) | \(1\) |
したがって,同じ文字が連続する文字列の個数は次の通りです。
以上より,同じ文字が連続して並ぶような文字列ができる確率は,次の通りです。
番号\(1\)のカードが\(1\)枚,\(2\)のカードが\(2\)枚,\(3\)のカードが\(3\)枚,\(4\)のカードが\(4\)枚あります。 これらのカードから無作為に\(3\)枚のカードを取り出します。 次の問いに答えてください。
-
取り出したカードが全て同じ番号である確率を求めてください。
-
取り出したカードが全て異なる番号である確率を求めてください。
答え
まずカードの取り出し方が全部で何通りあるか求めておくと,\(10\)枚から\(3\)枚を選ぶので,その場合の数は次の通りです。
-
\(3\)枚が同じ番号になるには,その番号は\(3\)か\(4\)である必要があります。
番号が全て\(3\)になる場合の数は,全ての\(3\)のカードを取り出すしかないので,\(1\)通りです。 番号が全て\(4\)になる場合の数は,\(4\)枚から\(3\)枚を選ぶので,\({}_4\mathrm{C}_3 = 4\)通りです。
したがって,取り出したカードが全て同じ番号である確率は,次の通りです。
\( \begin{align} \displaystyle\frac{1 + 4}{120} = \textcolor{red}{\displaystyle\frac{1}{24}} \end{align} \) -
選ばれない番号が\(1\)つだけあるということです。 場合分けして考えます。
[1] \(1\)以外の番号のカードを\(1\)枚ずつ取り出す場合,カードの取り出し方は次の数だけあります。
\( \begin{align} 2 \times 3 \times 4 = 24 \end{align} \)[2] \(2\)以外の番号のカードを\(1\)枚ずつ取り出す場合,カードの取り出し方は次の数だけあります。
\( \begin{align} 1 \times 3 \times 4 = 12 \end{align} \)[3] \(3\)以外の番号のカードを\(1\)枚ずつ取り出す場合,カードの取り出し方は次の数だけあります。
\( \begin{align} 1 \times 2 \times 4 = 8 \end{align} \)[4] \(4\)以外の番号のカードを\(1\)枚ずつ取り出す場合,カードの取り出し方は次の数だけあります。
\( \begin{align} 1 \times 2 \times 3 = 6 \end{align} \)以上,[1]~[4]より,取り出したカードが全て異なる番号である確率は,次の通りです。
\( \begin{align} \displaystyle\frac{24 + 12 + 8 + 6}{120} = \textcolor{red}{\displaystyle\frac{5}{12}} \end{align} \)
次の\(4 \times 4\)のマス目を見てください。

この\(16\)マスから無作為に\(3\)マスを選び,下図のように黒く塗ります。

このとき,黒く塗ったマスが全て「繋がる」確率を求めてください。 「繋がる」とは,どの黒マスから他のどの黒マスへも,白マスを介さずに上下左右の移動だけでたどり着けることを指すものとします。 上図は黒マスが繋がっている例です。
答え
まず黒マスの塗り方が全部で何通りあるのか確認しましょう。 \(16\)マスから\(3\)マスを選ぶので,その塗り方の数は次の通りです。
次に黒マスが繋がる塗り方を考えます。 \(3\)つの黒マスが繋がるのは,黒マスが次のどれかの形で塗られた場合です。
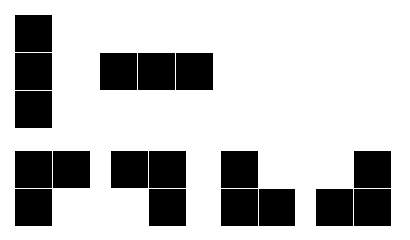
それぞれの形の塗り方が何通りあるかを数えれば,黒マスが繋がる塗り方が何通りあるか分かります。 それぞれの形のピースを\(4 \times 4\)のマス目にはめ込む方法の数を数えれば良いわけですね。
まず黒マスが一直線に並ぶ場合を考えましょう。 黒マスが縦に一直線に並ぶ塗り方であれば,次図の通り\(8\)通りあります。
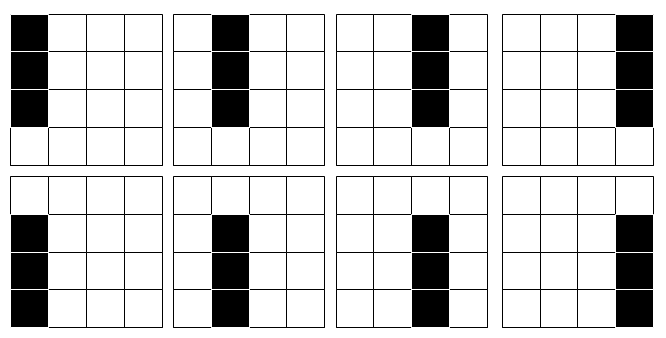
同様に黒マスが横に一直線に並ぶ塗り方も,\(8\)通りあります。
次に黒マスが折れ曲がって並ぶ場合を考えましょう。 左上に角がある場合の塗り方であれば,次図の通り\(9\)通りあります。

同様に他の黒マスが折れ曲がる塗り方も,\(9\)通りずつあります。
以上より,黒マスが繋がる塗り方は,次の数だけあります。
したがって,塗った黒マスが繋がる確率は,次の通りです。
